Выпуклость графика функции. Точки перегиба
Точки разрыва и экстремума функции в основном определяют поведение графика. Введем понятие других значимых для качества графика точек.
График дифференцируемой функции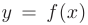 
называется выпуклым на интервале 
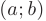, если он располагается ниже любой из своих касательных на этом интервале. В противном случае график функции 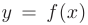называется вогнутым (выпуклым вниз) на интервале .
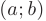Достаточное условие выпуклости вверх (вниз) графика функции. Если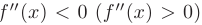 
на некотором промежутке 
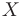, то график функции является выпуклым вверх (вниз) на этом промежутке.
Точка :го, в которой вторая производная дважды дифференцируемой функции равна нулю или не существует называется критической точкой второго рода.
Точкой перегиба графика функции называется точка при переходе через которую график функции меняет направление выпуклости.
Достаточное условие перегиба. Если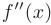 
при переходе через критическую точку второго рода 
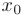меняет знак, то 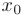есть точка перегиба графика функции 
.
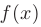Заметим, что если критическая точка первого рода не является точкой экстремума, то она есть точка перегиба.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Максимум и минимум функции в математике |
| Наибольшее и наименьшее значение функции на отрезке в математике |
| Функция многих переменных в математике |
| Непрерывность и частные производные в математике |
