Оглавление:
Вынужденные колебания материальной точки
Если материальную точку вывести из положения устойчивого равновесия и затем предоставить ее действию только восстанавливающей силы и силы сопротивления, то ее колебания будут постепенно затухать.
Рассмотрим теперь случай, когда на точку во все время ее движения действует еще и периодически изменяющаяся по модулю и направлению сила, называемая возмущающей силой. Возмущающей силой может быть сила, периодически изменяющаяся по любому закону. Мы ограничимся рассмотрением случая, практически наиболее важного, когда возмущающая сила изменяется по гармоническому закону.
По-прежнему примем прямую, вдоль которой движется точка 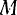 , за ось
, за ось 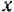 : и положение равновесия этой точки — за начало координат. Пусть на точку
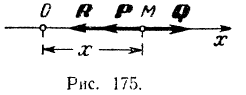
: и положение равновесия этой точки — за начало координат. Пусть на точку 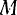 (рис. 175) действуют силы:
(рис. 175) действуют силы: 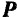 — восстанавливающая сила, модуль которой
— восстанавливающая сила, модуль которой 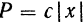 ,
, 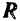 — сила сопротивления среды, модуль которой
— сила сопротивления среды, модуль которой 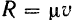 , и возмущающая сила
, и возмущающая сила 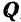 , проекция которой на ось
, проекция которой на ось 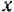 изменяется по гармоническому закону
изменяется по гармоническому закону
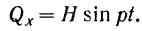
В равенстве (123) 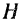 — амплитуда возмущающей силы,
— амплитуда возмущающей силы, 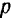 — круговая частота изменения возмущающей силы.
— круговая частота изменения возмущающей силы.
Проекция на ось 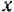 равнодействующей всех сил, действующих на точку
равнодействующей всех сил, действующих на точку 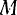 :
:
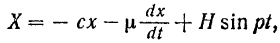
и дифференциальное уравнение движения этой точки принимает вид
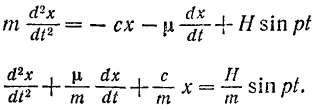
Обозначив
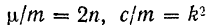
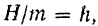
получим неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
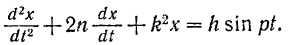
Как известно из теории дифференциальных уравнений, общее решение такого уравнения есть сумма двух слагаемых: общего решения 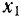 соответствующего однородного уравнения и частного решения
соответствующего однородного уравнения и частного решения 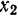 данного неоднородного уравнения:
данного неоднородного уравнения:
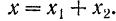
Общее решение однородного уравнения
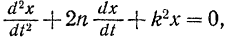
при условии, что 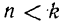 , нами ранее было уже найдено [равенство (121)]:
, нами ранее было уже найдено [равенство (121)]:
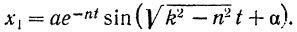
Ищем частное решение 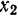 неоднородного уравнения (124) в виде
неоднородного уравнения (124) в виде
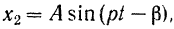
где 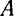 и
и 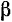 — некоторые постоянные, которые должны удовлетворять следующему условию: при подстановке выражения (III) в уравнение (124) последнее должно обращаться в тождество.
— некоторые постоянные, которые должны удовлетворять следующему условию: при подстановке выражения (III) в уравнение (124) последнее должно обращаться в тождество.
Вычислим первую и вторую производные по времени от выражения (III):
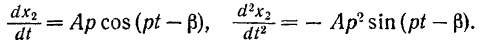
Подставляя значения (III) и (IV) в уравнение (124), получим:
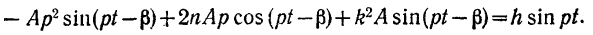
Обозначим для краткости:
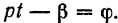
Отсюда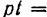
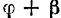 Подставив эти значения в предыдущее равенство, получим:
Подставив эти значения в предыдущее равенство, получим:
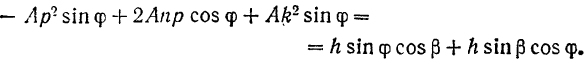
Перенося все члены последнего равенства в левую часть и группируя отдельно члены, содержащие 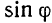 и
и 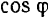 , будем иметь:
, будем иметь:
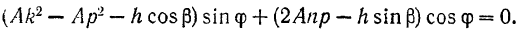
Последнее равенство должно быть справедливым для любого момента времени и, следовательно, при любых значениях аргумента
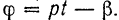
Это возможно лишь в том случае, когда коэффициенты при 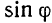 и
и 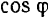 в равенстве (V) будут равны нулю. Отсюда получим следующую систему двух уравнений для определения
в равенстве (V) будут равны нулю. Отсюда получим следующую систему двух уравнений для определения 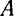 и
и 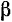 :
:
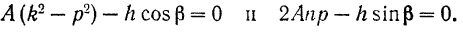
Переписав эти уравнения в виде
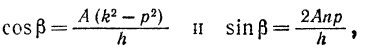
находим
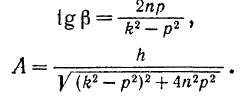
Подставляя найденные решения (II) и (III) в равенство (1), получим общее решение дифференциального уравнения (124):
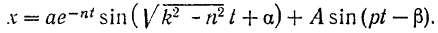
Входящие в это уравнение постоянные 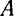 и
и 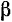 определяются по формулам (125) и (126), постоянные же
определяются по формулам (125) и (126), постоянные же 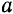 и
и 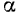 определяются по начальным условиям движения точки
определяются по начальным условиям движения точки 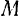 .
.
Первый член правой части равенства (127) определяет затухающие колебания точки 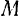 , а второй член — незатухающие гармонические колебания с амплитудой
, а второй член — незатухающие гармонические колебания с амплитудой 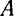 и частотой
и частотой 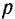 этой точки, обусловленные действием на нее возмущающей силы
этой точки, обусловленные действием на нее возмущающей силы  . Колебания, обусловленные действием на точку возмущающей силы, называются вынужденными.
. Колебания, обусловленные действием на точку возмущающей силы, называются вынужденными.
Как было выяснено ранее (стр. 268), амплитуды затухающих колебаний быстро уменьшаются, стремясь к нулю, и по прошествии некоторого времени, называемого временем установления, с этими колебаниями практически можно не считаться.
Таким образом, по прошествии времени установления движение точки 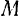 будет совершаться по закону:
будет совершаться по закону:
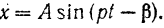
Уравнение (128) и служит уравнением вынужденных колебаний материальной точки  под действием на нее восстанавливающей силы
под действием на нее восстанавливающей силы 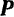 , пропорциональной расстоянию, силы сопротивления
, пропорциональной расстоянию, силы сопротивления 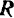 , пропорциональной первой степени скорости точки, и возмущающей силы
, пропорциональной первой степени скорости точки, и возмущающей силы 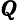 , изменяющейся по гармоническому закону и при условии, то
, изменяющейся по гармоническому закону и при условии, то
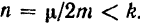
Из сравнения равенств (123) и (128) следует, что частота вынужденных колебаний равна частоте 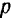 возмущающей силы. Следовательно, частота
возмущающей силы. Следовательно, частота 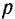 и период
и период 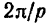 вынужденных колебаний не зависят ни от массы колебающейся точки, ни от величин коэффициентов
вынужденных колебаний не зависят ни от массы колебающейся точки, ни от величин коэффициентов 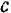 и
и 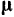 в выражениях восстанавливающей силы и силы сопротивления.
в выражениях восстанавливающей силы и силы сопротивления.
Из сравнения тех же равенств следует, что фаза 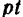 —
— 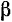 вынужденных колебаний отстает от фазы
вынужденных колебаний отстает от фазы 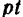 возмущающей силы на величину
возмущающей силы на величину 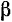 , называемую сдвигом фазы и определяемую формулой (125).
, называемую сдвигом фазы и определяемую формулой (125).
Исследуем теперь более подробно влияние сопротивления на амплитуду 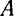 вынужденных колебаний.
вынужденных колебаний.
Из формулы (126) следует, что амплитуда 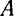 вынужденных колебаний уменьшается с увеличением коэффициента затухания
вынужденных колебаний уменьшается с увеличением коэффициента затухания
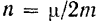
и, следовательно, с увеличением сопротивления движению точки.
При отсутствии сопротивления 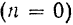 амплитуда вынужденных колебаний точки равна
амплитуда вынужденных колебаний точки равна
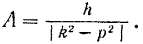
Найдем, как изменяется амплитуда
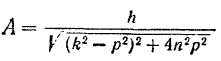
с изменением частоты 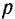 возмущающей силы (при данных значениях
возмущающей силы (при данных значениях
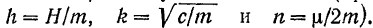
Максимум амплитуды будет соответствовать минимуму функции
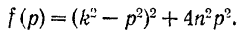
Первая производная этой функции
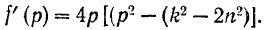
Так как всегда 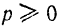 , то
, то
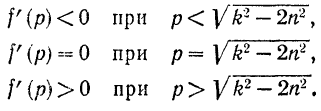
Следовательно, при 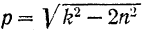 функция
функция 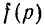 имеет минимум, а амплитуда
имеет минимум, а амплитуда 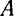 — максимум.
— максимум.
Значение частоты возмущающей силы, при котором амплитуда вынужденных колебаний имеет максимальное значение, называется критическим:
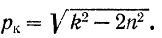
Как видно из формулы (130). критическая частота и максимум амплитуды существуют только при значениях коэффициента затухания 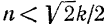 . Если
. Если 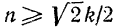 , то при всех значениях частоты
, то при всех значениях частоты 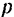 возмущающей силы первая производная
возмущающей силы первая производная 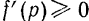 . Следовательно, при данных значениях
. Следовательно, при данных значениях 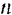 с увеличением частоты
с увеличением частоты 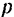 затухающих колебаний функция
затухающих колебаний функция 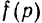 монотонно возрастает от значения
монотонно возрастает от значения 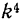 до
до  , а амплитуда колебаний монотонно убывает от значения
, а амплитуда колебаний монотонно убывает от значения 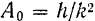 до нуля.
до нуля.
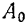 представляет собой величину статического отклонения точки
представляет собой величину статического отклонения точки 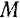 от начала координат
от начала координат 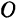 под действием постоянной силы, равной но модулю наибольшему значению
под действием постоянной силы, равной но модулю наибольшему значению 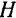 возмущающей силы
возмущающей силы  . Модуль восстанавливающей силы
. Модуль восстанавливающей силы 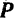 при отклонении точки
при отклонении точки 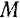 на величину
на величину 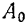 равен
равен 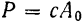 . В положении равновесия точки
. В положении равновесия точки 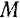 должно иметь место равенство
должно иметь место равенство 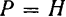 , т. е.
, т. е. 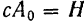 . Следовательно,
. Следовательно,
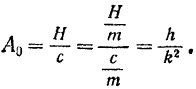
Подставляя критическое значение 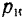 частоты возмещающей силы в формулу (124), будем иметь:
частоты возмещающей силы в формулу (124), будем иметь:
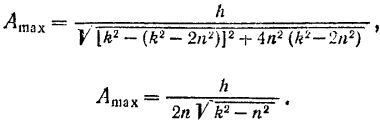
Отношение максимального значения амплитуды 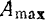 вынужденных колебаний к величине
вынужденных колебаний к величине 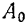 амплитуды при
амплитуды при 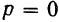 называется коэффициентом динамичности:
называется коэффициентом динамичности:
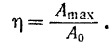
Из формул (131) и (132) следует, что коэффициент динамичности равен
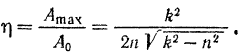
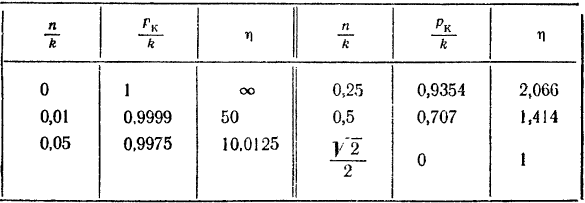
Ниже приводится таблица значений критической частоты 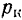 и коэффициента динамичности
и коэффициента динамичности 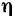 для различных значений отношения
для различных значений отношения 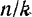 и построенный по этой таблице график
и построенный по этой таблице график 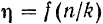 (рис. 176).
(рис. 176).
Случай, когда частота 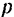 возмущающей силы близка по своему значению к частоте
возмущающей силы близка по своему значению к частоте 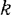 свободных колебаний точки, сопровождающийся значительным увеличением амплитуды вынужденных колебаний, называется резонансом.
свободных колебаний точки, сопровождающийся значительным увеличением амплитуды вынужденных колебаний, называется резонансом.
Из таблицы и графика видно, что при малом сопротивлении (при малых значениях коэффициента 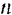 затухания) явление резонанса резко выражено, и амплитуда
затухания) явление резонанса резко выражено, и амплитуда 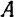 вынужденных колебаний может достигать весьма большой величины даже, при малой возмущающей силе (при малом
вынужденных колебаний может достигать весьма большой величины даже, при малой возмущающей силе (при малом 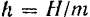 ).
).
При отсутствии сопротивления и совпадении частоты возмущающей силы с частотой свободных колебаний точки амплитуда вынужденных колебаний неограниченно возрастает, стремясь к бесконечности.
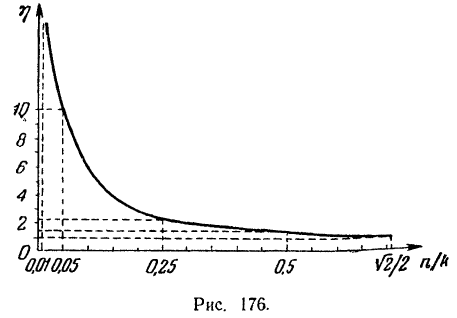
Отношение амплитуды 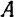 вынужденных колебаний при любой их частоте к амплитуде
вынужденных колебаний при любой их частоте к амплитуде 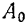 при частоте
при частоте 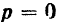 определяется, как это следует из формул (126) и (131), величиной
определяется, как это следует из формул (126) и (131), величиной
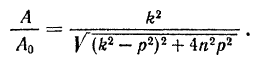
Если, пользуясь этим выражением, определить зависимость
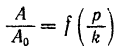
для значений
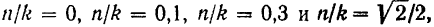
рафики этих функций будут иметь вид, представленный на рис. 177.
Из графиков видно, что:
Если 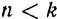 , то амплитуда вынужденных колебаний сначала возрастает до величины
, то амплитуда вынужденных колебаний сначала возрастает до величины 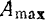 с увеличением частоты
с увеличением частоты 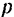 до критического значения
до критического значения 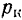 , а при дальнейшем увеличении частоты убывает, стремясь к нулю.
, а при дальнейшем увеличении частоты убывает, стремясь к нулю.
Если 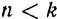 , то при значениях
, то при значениях 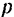 , много меньших или много больших
, много меньших или много больших 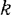 , влияние сопротивления на амплитуду вынужденных колебаний невелико и ее можно вычислять по формулам (129).
, влияние сопротивления на амплитуду вынужденных колебаний невелико и ее можно вычислять по формулам (129).
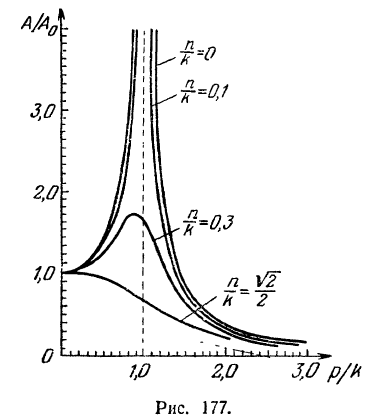
Амплитуду 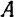 вынужденных колебаний можно получить сколь угодно малой даже при большой возмущающей силе (при большом значении
вынужденных колебаний можно получить сколь угодно малой даже при большой возмущающей силе (при большом значении 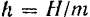 ), если частота
), если частота 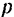 возмущающей силы будет много больше частоты
возмущающей силы будет много больше частоты 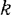 свободных колебаний точки.
свободных колебаний точки.
Пример задачи:
Двигатель весом 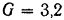 т установлен посредине двух двутавровых балок № 20,6, расположенных параллельно. Длина каждой балки
т установлен посредине двух двутавровых балок № 20,6, расположенных параллельно. Длина каждой балки  м, концы их свободно лежат на двух опорах. При каком числе оборотов двигателя можно ожидать появления резонанса, т. е. опасных колебаний балок с установленным на них двигателем? Весом балок пренебречь.
м, концы их свободно лежат на двух опорах. При каком числе оборотов двигателя можно ожидать появления резонанса, т. е. опасных колебаний балок с установленным на них двигателем? Весом балок пренебречь.
Решение:
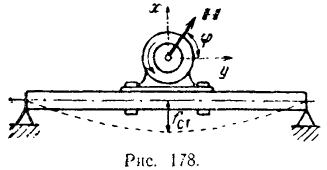
Вследствие неполной уравновешенности вращающихся частей двигателя на его вал будет действовать центробежная сила 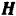 . При вращении вала проекция этой силы на вертикальную ось
. При вращении вала проекция этой силы на вертикальную ось 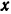 (рис. 178) изменяется по закону
(рис. 178) изменяется по закону 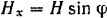 . При равномерном вращении вала угол его поворота
. При равномерном вращении вала угол его поворота 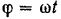 и, следовательно,
и, следовательно, 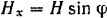 .
.
Таким образом, при работе двигателя на его вал (и балки) действует возмущающая сила 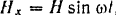 изменяющаяся по гармоническому закону. Частота
изменяющаяся по гармоническому закону. Частота 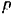 изменения этой силы равна угловой скорости вращения вала.
изменения этой силы равна угловой скорости вращения вала.
Как уже говорилось, резонанс наступает при совпадении периодов (а следовательно, и частот) свободных и вынужденных колебаний. Частота свободных колебаний балки
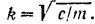
При статическом равновесии балки
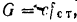
откуда
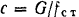
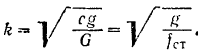
Статический прогиб балок, свободно лежащих на двух опорах и нагруженных определяем по соответствую средние сосредоточенной силой 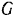 , по формуле сопротивления материалов:
, по формуле сопротивления материалов:
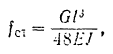
где
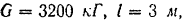
модуль упругости стали
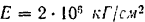
полный момент инерции площади поперечного сечения двух двутавровых балок № 20,6 (определяемый ГОСТом 10016-3!))
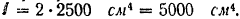
Подставляя эти данные, находим:
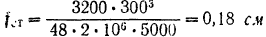
Частота свободных колебаний
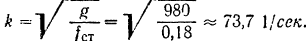
Критическая угловая скорость вала двигателя
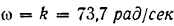
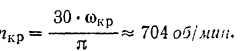
Двигатель должен работать при числе оборотов, значительно больших или значительно меньших 700 об/мин.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Свободные колебания материальной точки с примером решения |
| Затухающие колебания материальной точки с примером решения |
| Механическая система |
| Центр масс системы |

