Выделение полного квадрата (куба) для решения уравнений и неравенств

Выделение полного квадрата (куба)

Этот небольшой вспомогательный приём достаточно часто оказывается полезным при выполнении преобразований.

Пример №403.

Решить уравнение

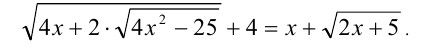
Решение:

Заметим, что выражение, стоящее под первым радикалом, является полным квадратом:

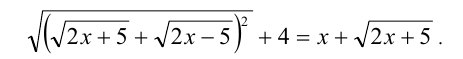
Упрощая, получаем уравнение

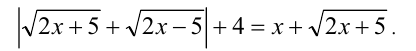
Так как под модулем стоит положительное выражение, то модуль можно опустить:

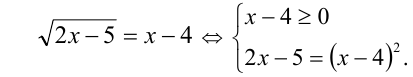
Ответ: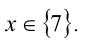

Пример №404.

Решить уравнение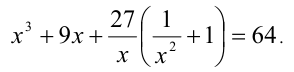

Решение:

Заметим, что в левой части уравнения находится полный куб:

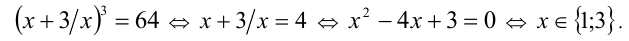
Пример №405.

Решить уравнение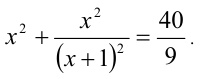

Решение:

Вычитая из обеих частей уравнения выражение 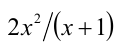и выделяя в левой части полный квадрат, получим:

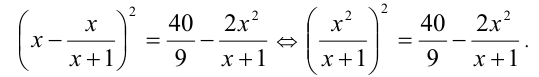
Сделав подстановку 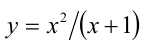, придём к квадратному уравнению

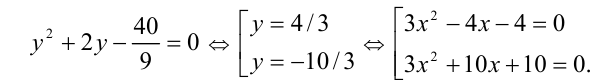
Ответ: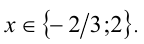

Пример №406.

Найти все значения параметра 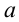, при каждом из которых уравнение

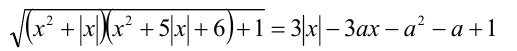
имеет корни, как большие 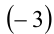, так и меньшие .

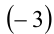Решение:

Покажем, что подкоренное выражение является полным квадратом:

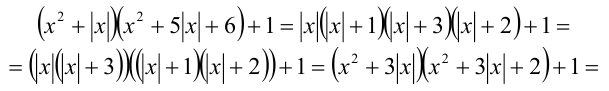
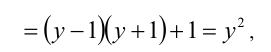
где 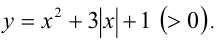Поэтому уравнение преобразуется к виду

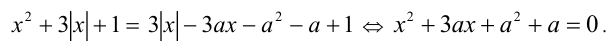
Левая часть полученного уравнения представляет собой квадратный трёхчлен 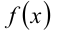с положительным старшим коэффи-циентом. Согласно методу парабол, он имеет корни, лежащие по разные стороны от числа 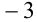, тогда и только тогда, когда

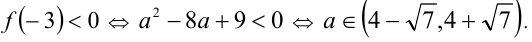
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Геометрический подход при решении уравнений

Формулы сокращённого умножения для решения уравнений и неравенств

Рассмотрение уравнения относительного некоторой величины

Натуральные и целые числа: определения, свойства, теоремы и законы