Оглавление:
Вычисление вычетов. Применение вычетов в вычислении интегралов
Правильные или устранимые особые точки. Очевидно, если  есть правильная или устранимая особая точка функции
есть правильная или устранимая особая точка функции  , то
, то 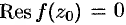 (в разложении Лорана (76.11) в этих случаях отсутствует главная часть, поэтому
(в разложении Лорана (76.11) в этих случаях отсутствует главная часть, поэтому 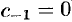 ).
).
Полюс. Пусть точка  является простым полюсом функции
является простым полюсом функции  . Тогда ряд Лорана для функции
. Тогда ряд Лорана для функции  в окрестности точки
в окрестности точки  имеет вид
имеет вид 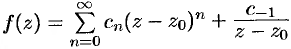 . Отсюда
. Отсюда
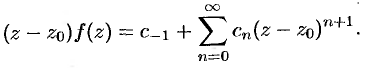
Поэтому, переходя в этом равенстве к пределу при 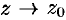 , получаем
, получаем
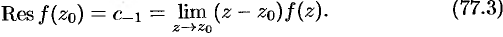
Замечание. Формуле (77.3) для вычисления вычета функции  в простом полюсе можно придать другой вид, если функция
в простом полюсе можно придать другой вид, если функция  является частным двух функций, аналитических в окрестностях точки
является частным двух функций, аналитических в окрестностях точки  .
.
Пусть 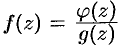 , где
, где 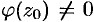 , a
, a 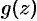 имеет простой нуль при
имеет простой нуль при  (т. е.
(т. е. 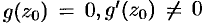 ). Тогда, применяя формулу (77.3), имеем:
). Тогда, применяя формулу (77.3), имеем: 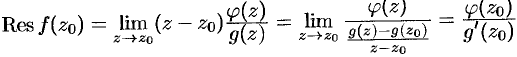 , т.е.
, т.е.
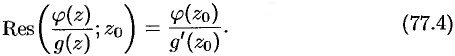
Пусть точка  является полюсом
является полюсом 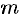 -го порядка функции
-го порядка функции  . Тогда лорановское разложение функции
. Тогда лорановское разложение функции  в окрестности точки
в окрестности точки  имеет вид
имеет вид
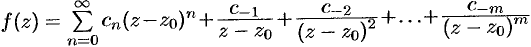
Отсюда
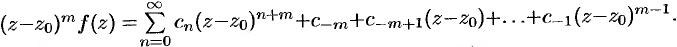
Дифференцируя последнее равенство (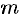 — 1) раз, получим:
— 1) раз, получим:
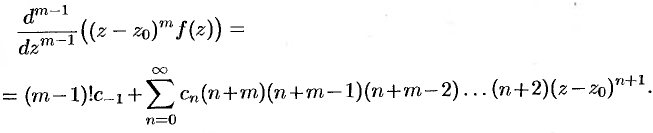
Переходя здесь к пределу при 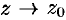 , получаем
, получаем
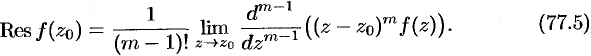
Существенно особая точка. Если точка  — существенно особая точка функции
— существенно особая точка функции  , то для вычисления вычета функции в этой точке обычно непосредственно определяют коэффициент
, то для вычисления вычета функции в этой точке обычно непосредственно определяют коэффициент 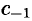 в разложении функции в ряд Лорана.
в разложении функции в ряд Лорана.
Пример №77.1.
Найти вычеты функции 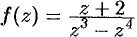 в ее особых точках.
в ее особых точках.
Решение:
Особыми точками функции  являются:
являются: 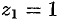 — простой полюс,
— простой полюс, 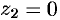 полюс третьего порядка (
полюс третьего порядка (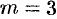 ). Следовательно, по формуле (77.4) имеем
). Следовательно, по формуле (77.4) имеем 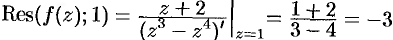 .
.
Используя формулу (77.5), находим:
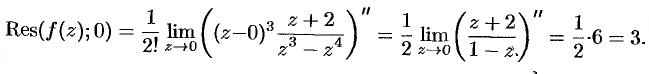
Пример №77.2.
Найти вычет функции 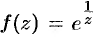 в особой точке
в особой точке 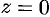 .
.
Решение:
Лорановское разложение данной функции в окрестности точки 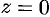 было найдено в примере 76.4. Из него находим
было найдено в примере 76.4. Из него находим 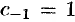 , т. е.
, т. е. 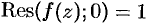 .
.
Теорема о вычетах часто используется для вычисления интеграла от функции комплексного переменного по замкнутому контуру.
Пример №77.3.
Вычислить 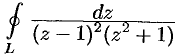 , где
, где  — окружность
— окружность 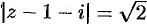 .
.
Решение:
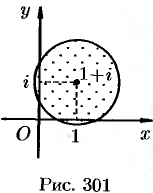
Функция 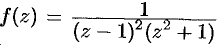 имеет в круге
имеет в круге 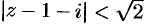 (см. рис. 301) простой полюс
(см. рис. 301) простой полюс 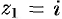 и полюс второго порядка
и полюс второго порядка 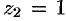 . Применяя формулы (77.2), (77.3) и (77.5), получаем:
. Применяя формулы (77.2), (77.3) и (77.5), получаем:
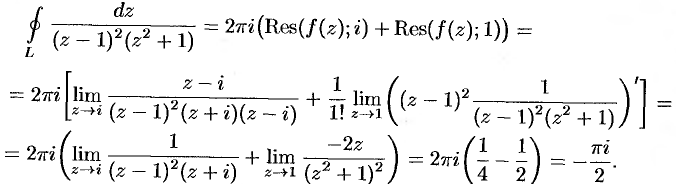
Определенный интеграл вида 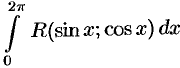 с помощью замены
с помощью замены 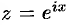 в некоторых случаях удается преобразовать в интеграл по замкнутому контуру
в некоторых случаях удается преобразовать в интеграл по замкнутому контуру 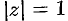 от функции комплексного переменного, к которому уже применима основная теорема о вычетах.
от функции комплексного переменного, к которому уже применима основная теорема о вычетах.
Пример №77.4.
Вычислить с помощью вычетов интеграл
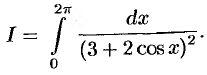
Решение:
Произведем замену переменного, положив 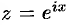 . Тогда
. Тогда 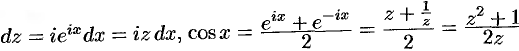 . При изменении
. При изменении  от 0 до
от 0 до  точка
точка  опишет в положительном направлении окружность
опишет в положительном направлении окружность  . Следовательно,
. Следовательно,
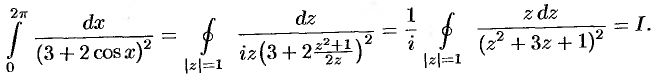
В круге 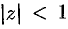 функция
функция 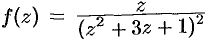 имеет полюс второго порядка
имеет полюс второго порядка 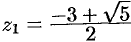 По формуле (77.5) находим
По формуле (77.5) находим
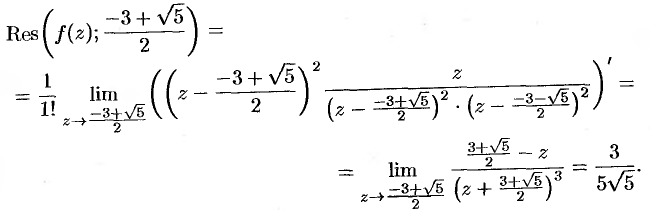
Следовательно, 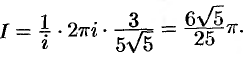
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Устранимые особые точки |
| Существенно особая точка |
| Свойства преобразования Лапласа |
| Обратное преобразование Лапласа |

