Оглавление:
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка 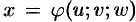 ,
, 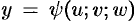 ,
, 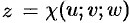 . Если эти функции имеют в некоторой области
. Если эти функции имеют в некоторой области 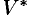 пространства
пространства 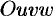 непрерывные частные производные и отличный от нуля определитель
непрерывные частные производные и отличный от нуля определитель
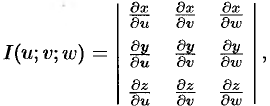
То справедлива формула замены переменных в тройном интеграле:
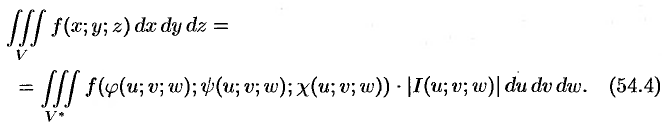
Здесь 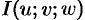 — определитель Якоби, или якобиан преобразования (примем без доказательства).
— определитель Якоби, или якобиан преобразования (примем без доказательства).
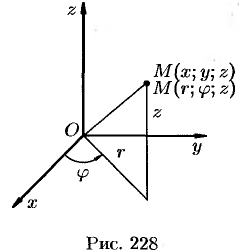
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
Положение точки 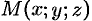 в пространстве
в пространстве 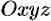 можно определить заданием трех чисел
можно определить заданием трех чисел 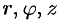 , где
, где 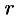 — длина радиуса-вектора проекции точки
— длина радиуса-вектора проекции точки  на плоскость
на плоскость 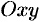 ,
, 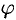 — угол, образованный этим радиусом-вектором с осью
— угол, образованный этим радиусом-вектором с осью  ,
,  — аппликата точки
— аппликата точки  (см. рис. 228).
(см. рис. 228).
Эти три числа (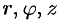 ) называются цилиндрическими координатами точки
) называются цилиндрическими координатами точки  .
.
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
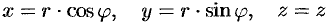
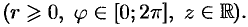
Возьмем в качестве 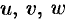 цилиндрические координаты
цилиндрические координаты 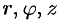 и вычислим якобиан преобразования:
и вычислим якобиан преобразования:
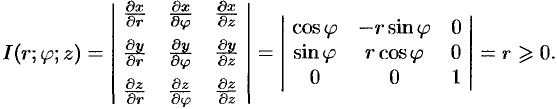
Формула замены переменных (54.4) принимает вид
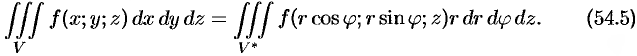
Таким образом, вычисление тройного интеграла приводится к интегрированию по 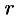 , по
, по 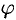 и по
и по  аналогично тому, как это делается в декартовых координатах.
аналогично тому, как это делается в декартовых координатах.
Замечание. К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
Пример №54.2.
Вычислить 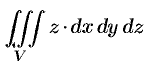 , где
, где  — область, ограниченная верхней частью конуса
— область, ограниченная верхней частью конуса 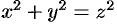 и плоскостью
и плоскостью 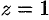 .
.
Решение:
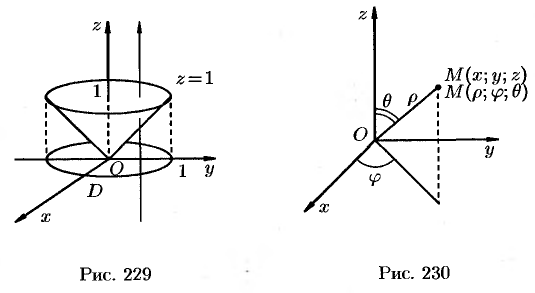
На рис. 229 изображена область интегрирования  . Вычислим интеграл путем перехода к цилиндрическим координатам:
. Вычислим интеграл путем перехода к цилиндрическим координатам: 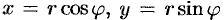 ,
, 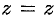 . Здесь
. Здесь 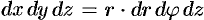 . Уравнение конуса примет вид
. Уравнение конуса примет вид 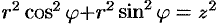 , т.е.
, т.е. 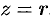 . Уравнение окружности
. Уравнение окружности 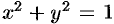 (границы области
(границы области  ) запишется так:
) запишется так: 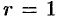 . Новые переменные изменяются в следующих пределах:
. Новые переменные изменяются в следующих пределах: 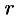 — от 0 до 1,
— от 0 до 1, 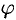 — от 0 до
— от 0 до 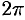 , a
, a  — от
— от 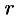 до 1 (прямая, параллельная оси
до 1 (прямая, параллельная оси 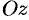 , пересекающая область
, пересекающая область  , входит в конус
, входит в конус 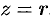 и выходит из него на высоте
и выходит из него на высоте 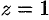 ).
).
Таким образом, согласно формуле (54.5), получаем:
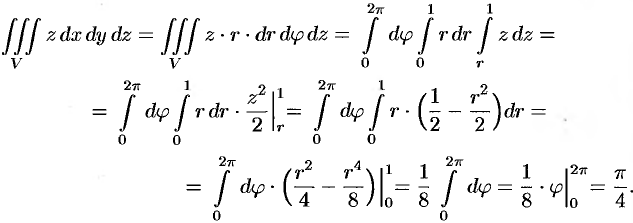
Заметим, что, не переходя к цилиндрическим координатам, получим:
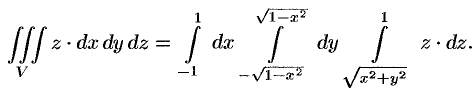
Сферическими координатами, точки 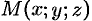 пространства
пространства 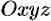 называется тройка чисел
называется тройка чисел 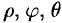 , где
, где 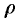 — длина радиуса-вектора точки
— длина радиуса-вектора точки  ,
, 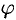 — угол, образованный проекцией радиуса-вектора
— угол, образованный проекцией радиуса-вектора 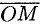 на плоскость
на плоскость 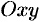 и осью
и осью  ,
, 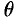 — угол отклонения радиуса-вектора
— угол отклонения радиуса-вектора 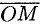 от оси
от оси 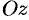 (см. рис. 230).
(см. рис. 230).
Сферические координаты 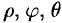 связаны с декартовыми координатами
связаны с декартовыми координатами 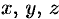 соотношениями:
соотношениями:
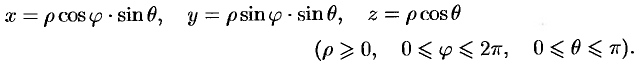
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
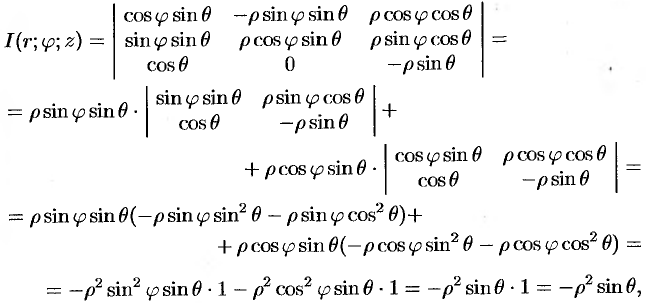
то
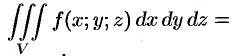
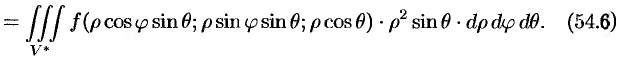
Замечание. Переходить к сферическим координатам удобно, когда область интегрирования  есть шар (уравнение его границы
есть шар (уравнение его границы 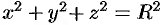 в сферических координатах имеет вид
в сферических координатах имеет вид 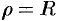 ) или его часть, а также если подынтегральная функция имеет вид
) или его часть, а также если подынтегральная функция имеет вид 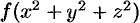 .
.
Пример №54.3.
Вычислить
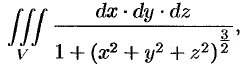
где  — шар
— шар 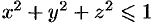 .
.
Решение:
Вычислим интеграл путем перехода к сферическим координатам: 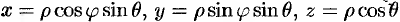 . Тогда
. Тогда
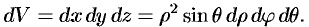
Граница области  — сфера и ее уравнение имеет вид
— сфера и ее уравнение имеет вид  , подынтегральная функция после замены переменных примет вид
, подынтегральная функция после замены переменных примет вид 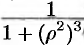 , т. е.
, т. е. 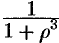 . Новые переменные изменяются в следующих пределах:
. Новые переменные изменяются в следующих пределах: 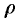 — от 0 до 1,
— от 0 до 1, 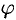 — от 0 до
— от 0 до 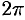 ,
, 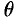 — от 0 до
— от 0 до 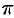 . Таким образом, согласно формуле (54.6),
. Таким образом, согласно формуле (54.6),
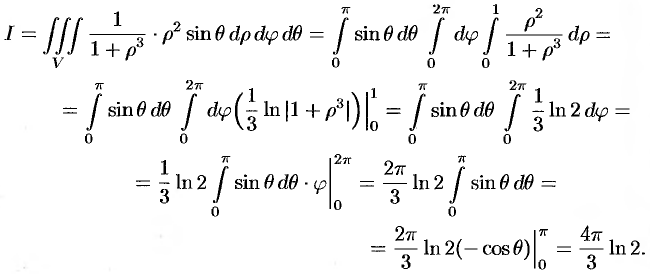
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Приложения двойного интеграла |
| Вычисление тройного интеграла в декартовых координатах |
| Некоторые приложения тройного интеграла |
| Вычисление криволинейного интеграла I рода |

