Оглавление:
Вычисление статических моментов и координат центра тяжести плоской кривой
Пусть на плоскости 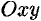 задана система материальных точек
задана система материальных точек 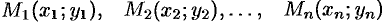 соответственно с массами
соответственно с массами 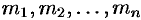 .
.
Статическим моментом 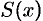 системы материальных точек относительно оси
системы материальных точек относительно оси  называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси
называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси  ):
): 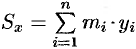 .
.
Аналогично определяется статический момент 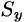 этой системы относительно оси
этой системы относительно оси 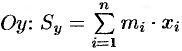 .
.
Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.
Пусть 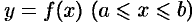 — это уравнение материальной кривой
— это уравнение материальной кривой 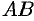 . Будем считать ее однородной с постоянной линейной плотностью
. Будем считать ее однородной с постоянной линейной плотностью 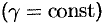 .
.
Для произвольного 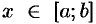 на кривой
на кривой 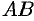 найдется точка с координатами
найдется точка с координатами 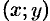 . Выделим на кривой элементарный участок длины
. Выделим на кривой элементарный участок длины 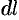 , содержащий точку
, содержащий точку 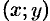 . Тогда масса этого участка равна
. Тогда масса этого участка равна 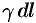 . Примем этот участок
. Примем этот участок 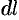 приближенно за точку, отстоящую от оси
приближенно за точку, отстоящую от оси 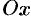 на расстоянии
на расстоянии 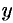 . Тогда дифференциал статического момента
. Тогда дифференциал статического момента 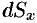 («элементарный момент») будет равен
(«элементарный момент») будет равен 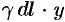 , т. е.
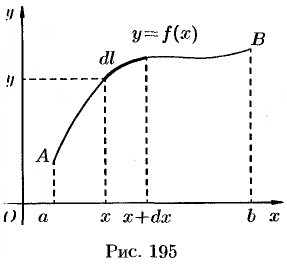
, т. е. 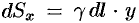 (см. рис. 195).
(см. рис. 195).
Отсюда следует, что статический момент 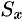 кривой
кривой 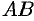 относительно оси
относительно оси 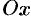 равен
равен
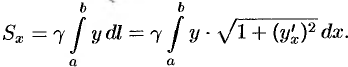
Аналогично находим 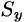 :
:
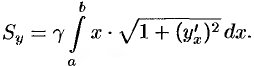
Статические моменты 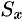 и
и 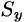 кривой позволяют легко установить положение ее центра тяжести (центра масс).
кривой позволяют легко установить положение ее центра тяжести (центра масс).
Центром тяжести материальной плоской кривой 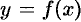 ,
, 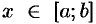 называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу
называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу 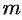 заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой
заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой 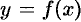 относительно той же оси. Обозначим через
относительно той же оси. Обозначим через 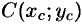 центр тяжести кривой
центр тяжести кривой 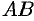 .
.
Из определения центра тяжести следуют равенства 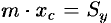 и
и 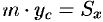 или
или 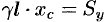 и
и 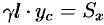 . Отсюда
. Отсюда 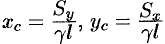 или
или
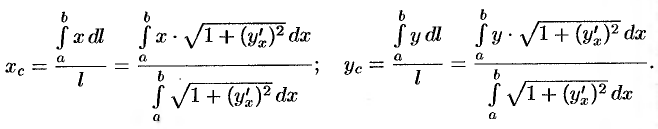
Пример №41.14.
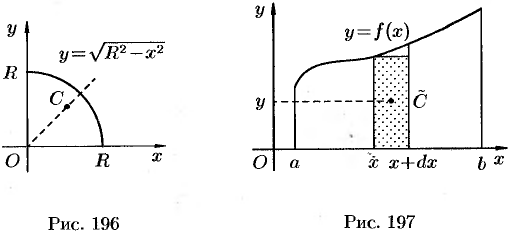
Найти центр тяжести однородной дуги окружности 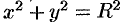 , расположенной в первой координатной четверти (см. рис. 196).
, расположенной в первой координатной четверти (см. рис. 196).
Решение:
Очевидно, длина указанной дуги окружности равна 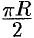 , т. е.
, т. е. 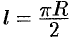 . Найдем статический момент ее относительно оси
. Найдем статический момент ее относительно оси 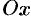 . Так как уравнение дуги есть
. Так как уравнение дуги есть 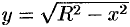 и
и 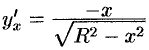 , то
, то 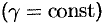 .
.
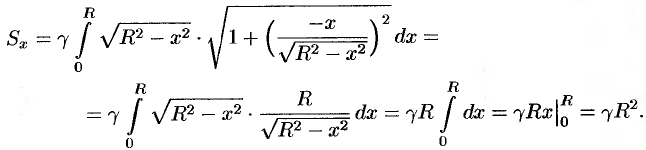
Стало быть,
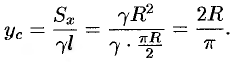
Так как данная дуга симметрична относительно биссектрисы первого координатного угла, то 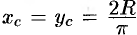 . Итак, центр тяжести имеет координаты
. Итак, центр тяжести имеет координаты 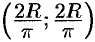 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

