Оглавление:
Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская фигура (пластинка), ограниченная кривой 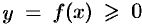 и прямыми
и прямыми 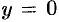 ,
, 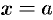 ,
, 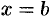 (см. рис. 197).
(см. рис. 197).
Будем считать, что поверхностная плотность пластинки постоянна 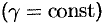 . Тогда масса всей пластинки равна
. Тогда масса всей пластинки равна 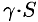 , т. е.
, т. е. 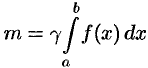 .
.
Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.
Тогда масса его равна 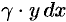 . Центр тяжести
. Центр тяжести 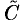 прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка
прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка 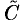 отстоит от оси
отстоит от оси 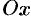 на
на 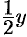 от оси
от оси 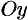 на
на 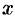 (приближенно; точнее на расстоянии
(приближенно; точнее на расстоянии 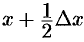 ). Тогда для элементарных статических моментов относительно осей
). Тогда для элементарных статических моментов относительно осей  и
и 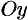 выполнены соотношения
выполнены соотношения
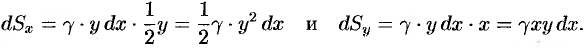
Следовательно, 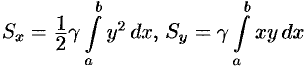 .
.
По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через 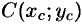 , что
, что 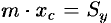 ,
, 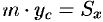 . Отсюда
. Отсюда
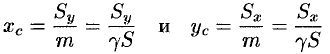
или
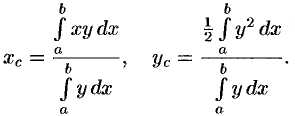
Пример №41.15.
Найдем координаты центра тяжести полукруга 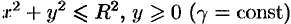 (см. рис. 198).
(см. рис. 198).
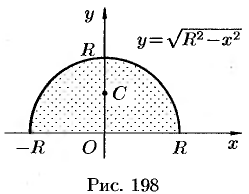
Решение:
Очевидно (ввиду симметрии фигуры относительно оси 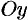 ), что
), что 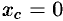 . Площадь полукруга равна
. Площадь полукруга равна 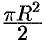 . Находим
. Находим 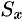 :
:
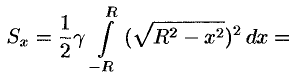
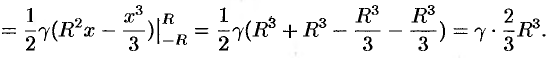
Стало быть,
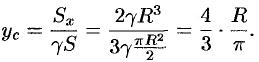
Итак, центр тяжести имеет координаты 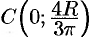 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

