Оглавление:
При вычислении пределов от показательно-степенной функции пользуются либо формулой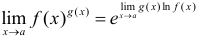 
, либо вторым замечательным пределом.
Пример №1.
Вычислить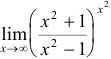 
.
Решение:
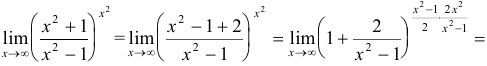
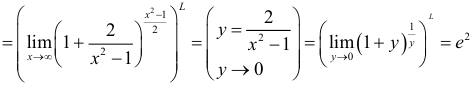, так как
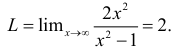
Пример №1.
Вычислить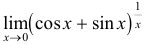 
.
Решение:
Заметим, что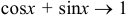 
, а 
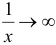при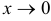 
. Следовательно, имеется неопределенность вида 
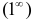. Для ее раскрытия воспользуемся вторым замечательным пределом. Получим, что
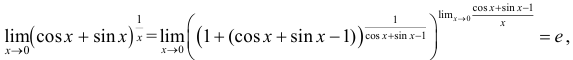
так как
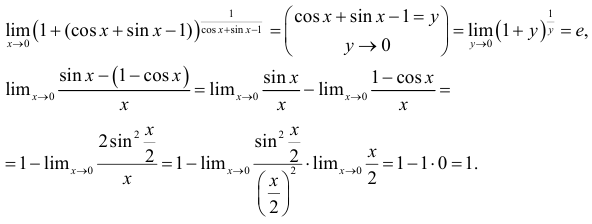
Пример №2.
Вычислить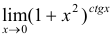 
.
Решение:
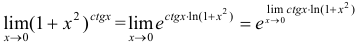в силу непрерывности 
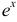. Вычислим
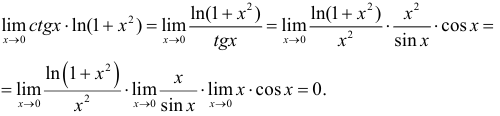
Следовательно,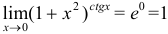 
.
Пример №3.
Вычислить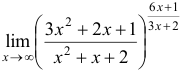 
.
Решение:
Так как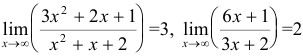 
, то в данном случае отсутствует неопределенность и
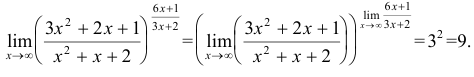
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Вычисление пределов, содержащих радикалы |
| Вычисление пределов, содержащих тригонометрические функции |
| Вычисление пределов с учетом их особенностей |
| Непрерывность функции в точке |
