Предел элементарной функции 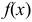 при
при 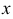 , стремящемся к значению
, стремящемся к значению 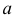 (
(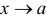 ), которое входит в область ее определения, равен частному значению функции при
), которое входит в область ее определения, равен частному значению функции при 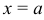 , т.е.
, т.е. 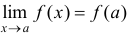 .
.
Если аргумент стремится к бесконечности или к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.
Рассмотрим основные свойства пределов:
1) Если существуют пределы функций 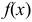 и
и 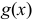 при
при 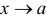 , то
, то
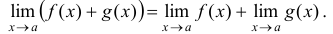
2) Если существуют пределы функций 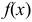 и
и 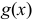 при
при 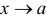 , то
, то
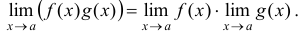
3) Постоянный множитель можно выносить за знак предела, т.е.
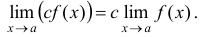
4) Если существует предел функции 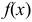 при
при 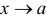 , то
, то
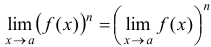 , где
, где 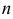 — натуральное число.
— натуральное число.
5) Если существуют пределы функций 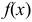 и
и 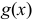 при
при 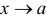 , причем предел функции
, причем предел функции 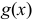 отличен от нуля, то
отличен от нуля, то
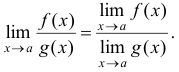
При вычислении пределов часто используют два замечательных предела:
1. 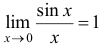 или
или 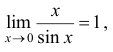
2. 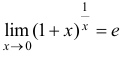 или
или 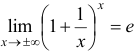
и их следствия:
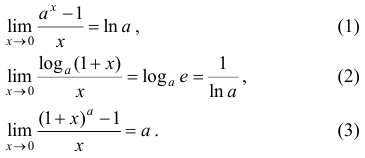
Второй замечательный предел используют для раскрытия неопределенностей вида 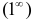 , а остальные — для неопределенности вида
, а остальные — для неопределенности вида 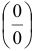 .
.
Вычисление пределов значительно упрощается при использовании эквивалентности бесконечно малых.
Функция 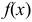 называется бесконечно малой при
называется бесконечно малой при 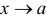 , если
, если 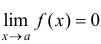 .
.
Функция 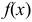 называется бесконечно большой при
называется бесконечно большой при 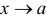 , если
, если 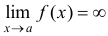 .
.
Свойства бесконечно малых и бесконечно больших:
1) Если 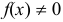 и
и 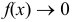 при
при 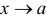 , то
, то 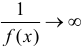 при
при 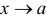 .
.
2) Если 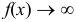 при
при 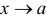 , то
, то 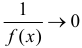 при
при 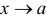 .
.
3) Если 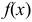 — бесконечно малая при
— бесконечно малая при 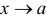 , a
, a 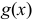 — ограниченная в некоторой окрестности точки
— ограниченная в некоторой окрестности точки 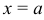 , то
, то 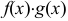 — бесконечно малая функция при
— бесконечно малая функция при 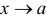 .
.
Две бесконечно малые функции называются эквивалентными (~), если предел их отношения равен 1. С помощью замечательных пределов можно доказать справедливость цепочки эквивалентных бесконечно малых 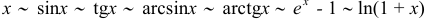 при
при 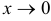 .
.
При раскрытии неопределенностей вида 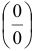 или
или 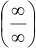 рекомендуется пользоваться указанными замечательными пределами либо пытаться сократить числитель и знаменатель на общие (критические) множители.
рекомендуется пользоваться указанными замечательными пределами либо пытаться сократить числитель и знаменатель на общие (критические) множители.
При вычислении пределов нередко пользуются правилом Лопиталя:
Пусть при вычислении предела 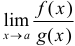 возникает неопределенность вида
возникает неопределенность вида 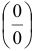 или
или  , но при этом существует
, но при этом существует 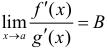 . Тогда
. Тогда 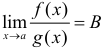 .
.
Использование правила Лопиталя в большинстве случаев значительно упрощает вычисление пределов, поэтому, прежде чем приступать к вычислению пределов, необходимо повторить правила вычисления производных.
Пример:
Найти пределы функций:
а) 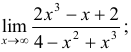 б)
б) 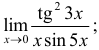
в) 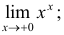 г)
г) 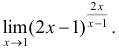
Решение:
а) Разделив числитель и знаменатель на большую степень 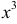 получим
получим
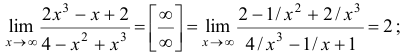
б) Умножив числитель и знаменатель на 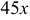 и используя первый замечательный предел, получим
и используя первый замечательный предел, получим
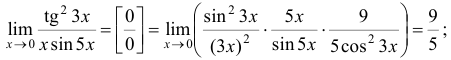
в) Логарифмируя и используя правило Лопиталя, получим
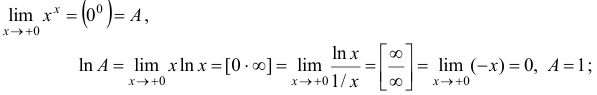
г) Сделав замену переменных и используя второй замечательный предел, получим
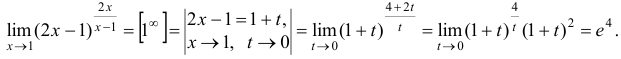
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Исследование общего уравнения кривой 2-го порядка |
| Функция |
| Вычисление пределов от рациональной дроби при x > a (a ≠ ∞ ) |
| Вычисление пределов от рациональной дроби при x > ∞ |

