Оглавление:
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области 
— проекции поверхности 
на плоскость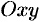 
.
Разобьем поверхность на части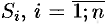 
. Обозначим через проекцию 
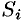на плоскость 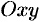. При этом область , окажется разбитой на 
частей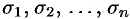 
. Возьмем в 
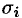произвольную точку 
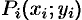и восстановим перпендикуляр к плоскости 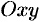до пересечения с поверхностью . Получим точку 
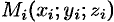на поверхности 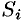. Проведем в точке 
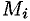касательную плоскость и рассмотрим ту ее часть 
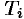, которая на плоскость 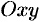проектируется в область 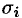(см. рис. 247). Площади элементарных часте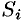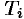й , и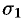 
обозначим как 
, 
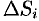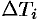и 
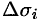соответственно. Будем приближенно считать, что
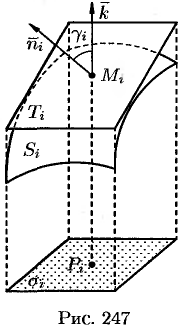
Обозначив через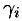 
острый угол между осью 
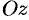и нормалью 
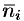к поверхности в точке 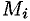, получаем:
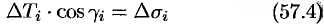
(область 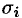есть проекция 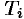на плоскость ).
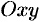Если поверхность задана уравнением 
, то, как известно (см. (45.2)), уравнение касательной плоскости в точке 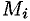есть
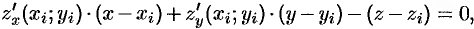
где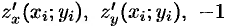 
— координаты нормального вектора к плоскости. Острый угол 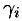есть угол между векторам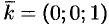и 
и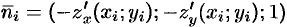 
.
Следовательно,
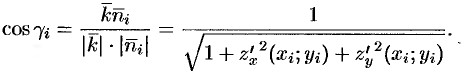
Равенство (57.4) принимает вид
В правой части формулы (57.2) заменим 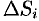(учитывая (57.3)) на полученное выражение для 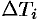, a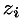 
заменим на 
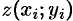. Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра 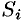(а следовательно, и 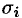), получаем формулу
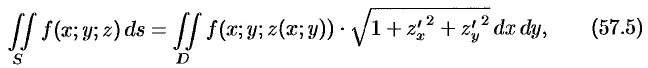
выражающую интеграл по поверхности через двойной интеграл по проекции на плоскость .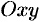
Отметим, что если поверхность задана уравнением вида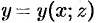 
или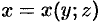 
, то аналогично получим:
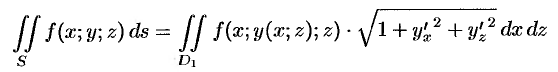
и
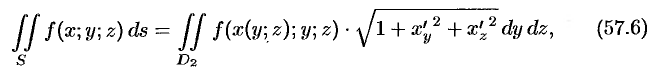
где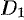 
и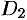 
— проекции поверхности на координатные плоскости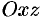 
и 
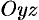соответственно.
Пример №57.1.
Вычислить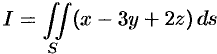 
, где — часть плоскости 
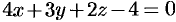, расположенной в I октанте (см. рис. 248).
Решение:
Запишем уравнение плоскости в виде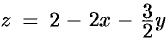 
. Находим 
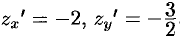. По формуле (57.5) имеем:
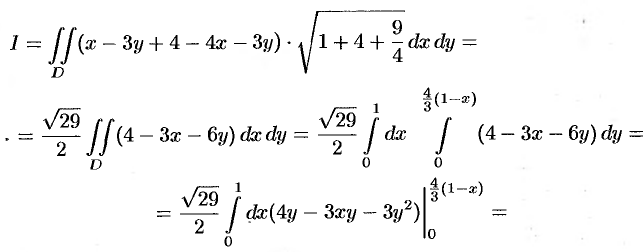
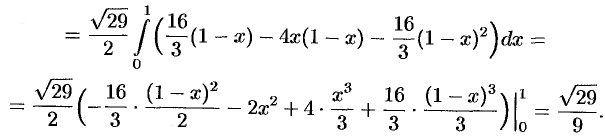
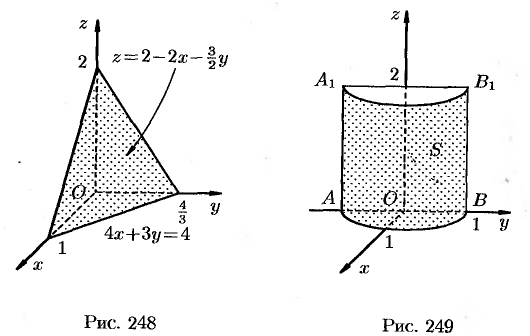
Пример №57.2.
Вычислить
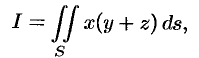
где — часть цилиндрической поверхности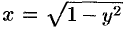 
, отсеченной плоскостями 
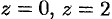(см. рис. 249).
Решение:
Воспользуемся формулой (57.6). Поскольку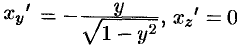 
, то
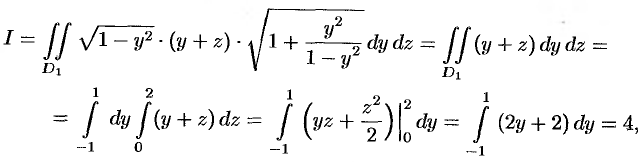
где 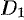— прямоугольник 
.
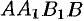На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
