Оглавление:
Вычисление площади поверхности вращения
Пусть кривая 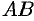 является графиком функции
является графиком функции 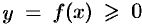 , где
, где 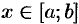 , а функция
, а функция 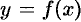 и ее производная
и ее производная 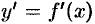 непрерывны на этом отрезке.
непрерывны на этом отрезке.
Найдем площадь 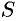 поверхности, образованной вращением кривой
поверхности, образованной вращением кривой 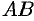 вокруг оси
вокруг оси  .
.
Применим схему II (метод дифференциала).
1. Через произвольную точку 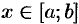 проведем плоскость
проведем плоскость 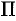 , перпендикулярную оси
, перпендикулярную оси  . Плоскость
. Плоскость 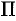 пересекает поверхность вращения по окружности с радиусом
пересекает поверхность вращения по окружности с радиусом  (см. рис. 191). Величина
(см. рис. 191). Величина 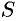 поверхности части фигуры вращения, лежащей левее плоскости, является функцией от
поверхности части фигуры вращения, лежащей левее плоскости, является функцией от  , т.е.
, т.е. 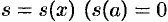 и
и 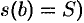 .
.
2. Дадим аргументу  приращение
приращение 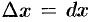 . Через точку
. Через точку 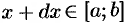 также проведем плоскость, перпендикулярную оси
также проведем плоскость, перпендикулярную оси  . Функция
. Функция 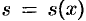 получит приращение
получит приращение 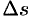 , изображенного на рисунке в виде «пояска».
, изображенного на рисунке в виде «пояска».
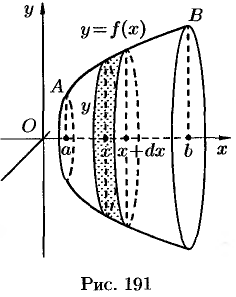
Найдем дифференциал площади 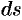 , заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна
, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна 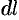 , а радиусы оснований равны
, а радиусы оснований равны 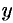 и
и 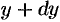 . Площадь его боковой поверхности равна
. Площадь его боковой поверхности равна 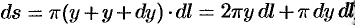 . Отбрасывая произведение
. Отбрасывая произведение 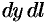 как бесконечно малую высшего порядка, чем
как бесконечно малую высшего порядка, чем 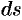 , получаем
, получаем 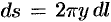 , или, так как
, или, так как 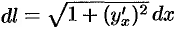 , то
, то 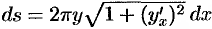 .
.
3. Интегрируя полученное равенство на пределах от 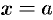 до
до 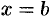 , получаем
, получаем
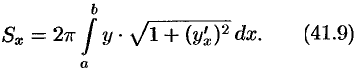
Если кривая 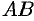 задана параметрическими уравнениями
задана параметрическими уравнениями 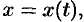
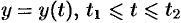 , то формула (41.9) для площади поверхности вращения принимает вид
, то формула (41.9) для площади поверхности вращения принимает вид
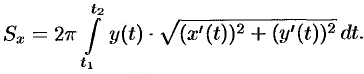
Пример 41.8.
Найти площадь поверхности шара радиуса 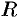 .
.
Решение:
Можно считать, что поверхность шара образована вращением полуокружности 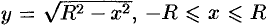 , вокруг оси
, вокруг оси  . По формуле (41.9) находим
. По формуле (41.9) находим
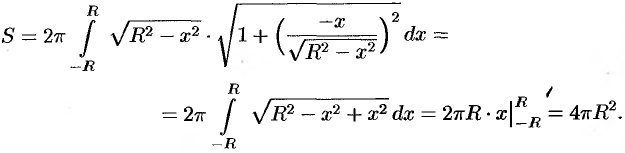
Дополнительный пример №41.9.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление длины дуги плоской кривой |
| Вычисление объема тела |
| Работа переменной силы |
| Приближенное вычисление определенного интеграла |

