Оглавление:
Вычисление площадей плоских фигур
Прямоугольные координаты
Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (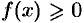
), равна соответствующему определенному интегралу:
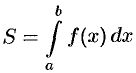или 
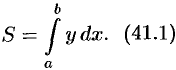
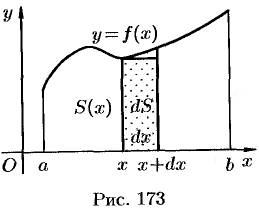
Формула (41.1) получена путем применения схемы I — метода сумм. Обоснуем формулу (41.1), используя схему II. Пусть криволинейная трапеция ограничена линиями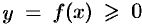 
, 
, 
, 
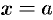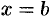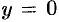(см. рис. 173). Для нахождения площади 
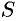этой трапеции проделаем следующие операции:
1. Возьмем произвольное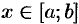 
и будем считать, что 
.
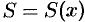2. Дадим аргументу 
приращение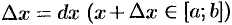 
. Функция 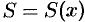получит приращение 
, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади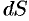 
есть главная часть приращения при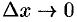 
, и, очевидно, он равен площади прямоугольника с основанием 
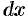и высотой 
.
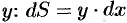3. Интегрируя полученное равенство в пределах от 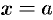до 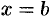, получаем 
.
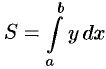Отметим, что если криволинейная трапеция расположена «ниже» оси 
, то ее площадь может быть найдена по формуле
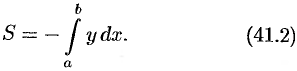
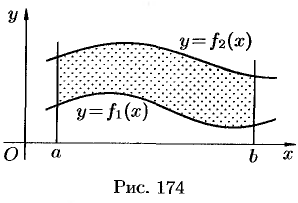
Формулы (41.1) и (41.2) можно объединить в одну:
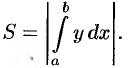
Площадь фигуры, ограниченной кривыми 
и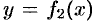 
, прямым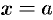и и 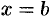(при условии 
) (см. рис. 174), можно найти по формуле
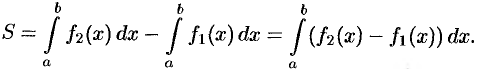
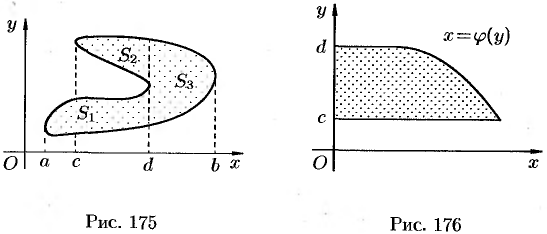
Если плоская фигура имеет «сложную» форму (см. рис. 175), то прямыми, параллельными оси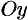 
, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.
Если криволинейная трапеция ограничена прямыми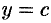 
и 
, осью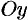 
и непрерывной кривой 
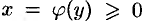(см. рис. 176), то ее площадь находится по формуле 
.
И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически
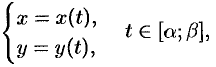
прямым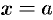и и 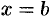и осью 
, то площадь ее находится по формуле
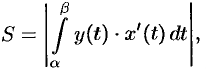
где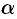 
и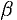 
определяются из равенств 
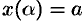и 
.
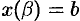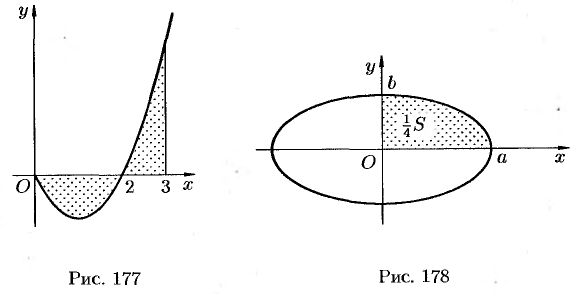
Пример №41.1.
Найти площадь фигуры, ограниченной осью и графиком функции 
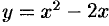при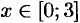 
.
Решение:
Фигура имеет вид, изображенный на рисунке 177. Находим ее площадь :
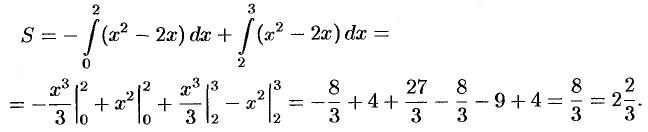
Дополнительный пример №41.2.
Полярные координаты
Найдем площадь 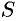криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией 
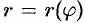и двумя лучами 
и 
, где 
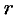и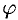 
— полярные координаты (см. рис. 179). Для решения задачи используем схему II — метод дифференциала.
1. Будем считать часть искомой площади S как функцию угла 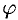, т. е. 
, где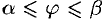 
(если , то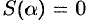 
, если 
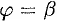, то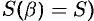 
.
2. Если текущий полярный угол 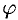получит приращение 
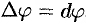, то приращение площади равно площади «элементарного криволинейного сектора»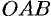 
.
Дифференциал 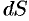представляет собой главную часть приращения при 
и равен площади кругового сектора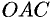 
(на рисунке она заштрихована) радиуса 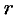с центральным углом 
. Поэтому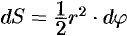 
.
3. Интегрируя полученное равенство в пределах от до , получим искомую площадь
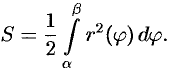
Пример №41.3.
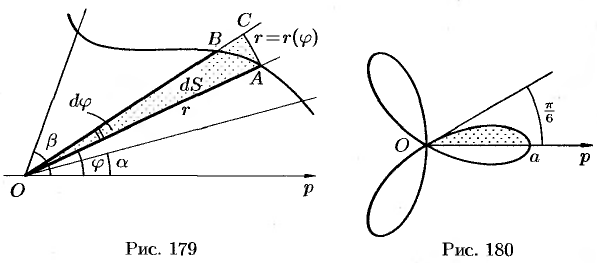
Найти площадь фигуры, ограниченной «трехлепестковой розой» 
(см. рис. 180).
Решение:
Найдем сначала площадь половины одного лепестка «розы», т. е.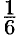 
часть всей площади фигуры:
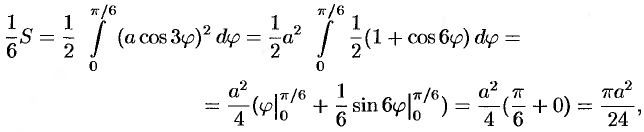
т. е.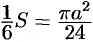 
. Следовательно, 
.
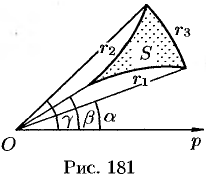
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 181, имеем:
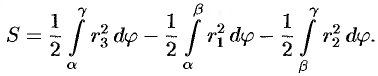
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интеграл от разрывной функции |
| Схемы применения определенного интеграла |
| Вычисление длины дуги плоской кривой |
| Вычисление объема тела |
