Оглавление:
Вычисление площадей фигур
С помощью определённого интеграла будем вычислять площади плоских фигур.
1. Площадь плоской фигуры, ограниченной непрерывными линиями 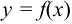 , ординатами
, ординатами 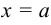 ,
, 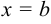 и отрезками оси абсцисс, выражается
и отрезками оси абсцисс, выражается
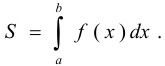
2. Площадь фигуры, ограниченной прямыми 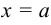 ,
, 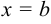 и двумя непрерывными кривыми
и двумя непрерывными кривыми  , вычисляется по формуле
, вычисляется по формуле
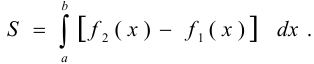
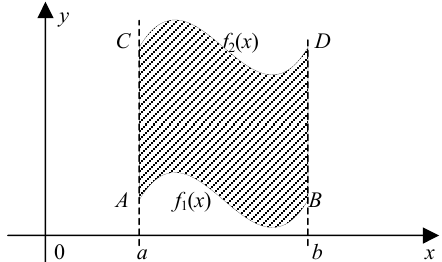
Задача №95.
Вычислить площадь фигуры, ограниченной линиями 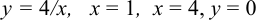 .
.
Решение:
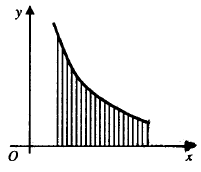
Эта фигура является криволинейной трапецией.
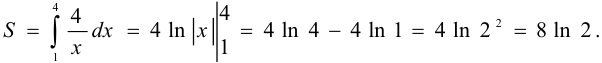
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

