Оглавление:
Рассмотрим примеры вычисления объемов геометрических тел с помощью двойного интеграла.
Пример №30.1.
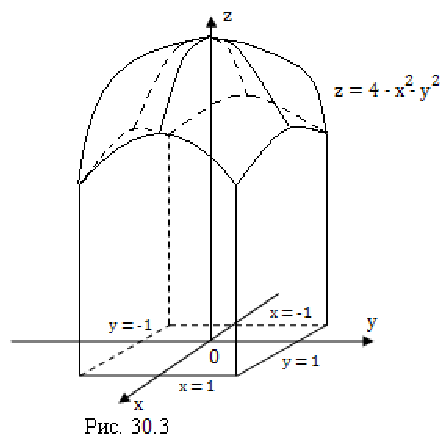
Найдите объем цилиндрического тела, изображенного на рис. 30.3, ограниченного сверху поверхностью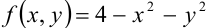 
, снизу — плоскостью 
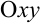, с боков — плоскостями 
.
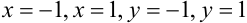Решение:
Поскольку геометрически двойной интеграл от неотрицательной функции равен объему цилиндрического тела, будем использовать формулу: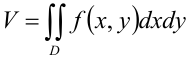 
.
В нашем случае 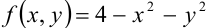. Область интегрирования 
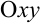, что хорошо видно на рис.30.3., представляет собой фигуру на плоскости , ограниченную прямыми 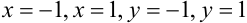, т.е. является прямоугольной областью. Следовательно, для нахождения объема данного цилиндрического тела надо вычислить двойной интеграл по прямоугольной области, т.е.
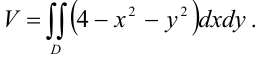
Будем использовать соответствующую формулу сведения двойного интеграла к повторному:
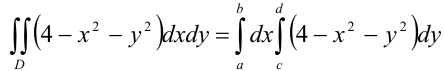
где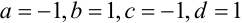 
.
Таким образом,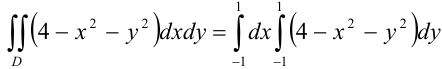 
.
Вычислим полученный повторный интеграл:
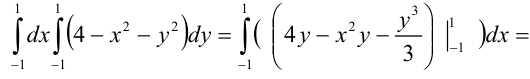
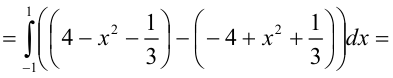
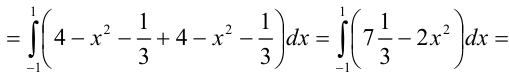
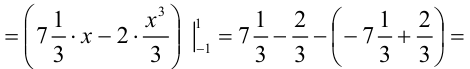
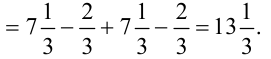
В итоге,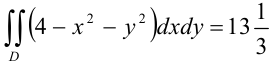 
. Следовательно, 
.
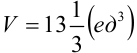Ответ: .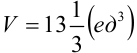
Пример №30.2.
Найдите объем цилиндрического тела, ограниченного сверху поверхностью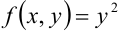 
, снизу — областью плоскости 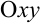, представляющей собой прямоугольный треугольник, образованный координатными осями и прямой 
.
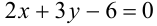Решение:
В силу геометрического смысла двойного интеграла от неотрицательной функции, для нахождения объема цилиндрического тела будем использовать формулу:
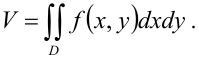
Вычислим двойной интеграл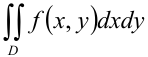 
по области . Для этого построим область интегрирования в прямоугольной декартовой системе координат на плоскости. Составим уравнение прямой 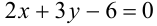с угловым коэффициентом: 
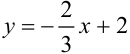. Построим эту прямую по двум точкам:
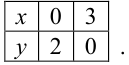
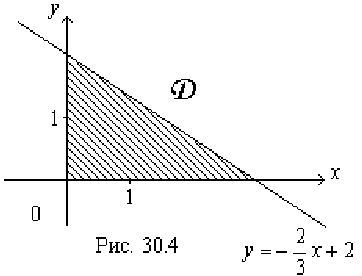
Изображённая на рис. 30.4. область интегрирования является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
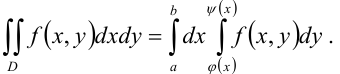
В нашем случае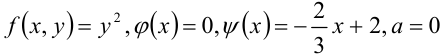 
.
Найдем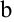 
как абсциссу точки пересечения прямой 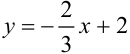с осью 
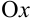, решив уравнение: 
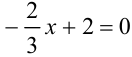. Получим 
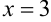, значит 
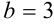. Следовательно,
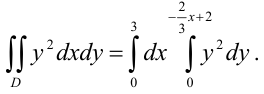
Вычислим полученный повторный интеграл:
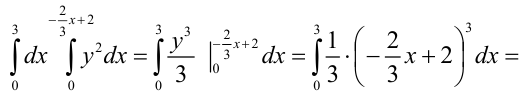
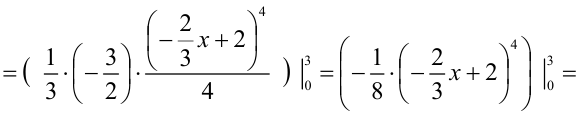
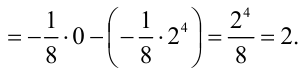
В итоге,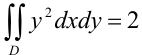 
. Следовательно, 
.
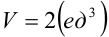Ответ: .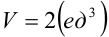
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
