Оглавление:
Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем 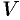 тела, причем известны площади
тела, причем известны площади 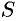 сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси
сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси  :
: 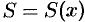 ,
, 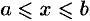 .
.
Применим схему II (метод дифференциапа).
1. Через произвольную точку 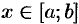 проведем плоскость
проведем плоскость 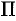 , перпендикулярную оси
, перпендикулярную оси  (см. рис. 187). Обозначим через
(см. рис. 187). Обозначим через 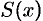 площадь сечения тела этой плоскостью;
площадь сечения тела этой плоскостью; 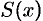 считаем известной и непрерывно изменяющейся при изменении
считаем известной и непрерывно изменяющейся при изменении  . Через
. Через 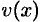 обозначим объем части тела, лежащее левее плоскости
обозначим объем части тела, лежащее левее плоскости 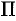 . Будем считать, что на отрезке
. Будем считать, что на отрезке 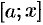 величина
величина 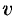 есть функция от
есть функция от  , т. е.
, т. е. 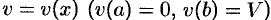 .
.
2. Находим дифференциал 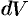 функции
функции 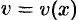 . Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось
. Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось  в точках
в точках  и
и 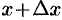 , который приближенно может быть принят за цилиндр с основанием
, который приближенно может быть принят за цилиндр с основанием 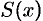 и высотой
и высотой 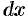 . Поэтому дифференциал объема
. Поэтому дифференциал объема 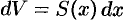 .
.
3. Находим искомую величину 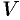 путем интегрирования
путем интегрирования 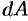 в пределах от
в пределах от 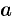 до
до 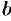 :
:
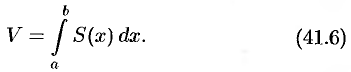
Полученная формула называется формулой объема тела по площади параллельных сечений.
Пример №41.6.
Найти объем эллипсоида 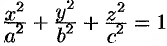 .
.
Решение:
Рассекая эллипсоид плоскостью, параллельной плоскости 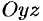 и на расстоянии
и на расстоянии  от нее
от нее 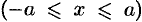 , получим эллипс (см. рис. 188):
, получим эллипс (см. рис. 188):
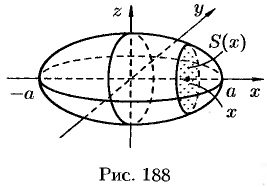
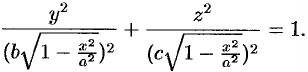
Площадь этого эллипса равна 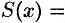
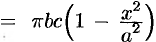 . Поэтому, по формуле (41.6), имеем
. Поэтому, по формуле (41.6), имеем
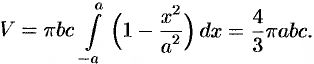
Объем тела вращения
Пусть вокруг оси  вращается криволинейная трапеция, ограниченная непрерывной линией
вращается криволинейная трапеция, ограниченная непрерывной линией 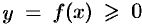 , отрезком
, отрезком 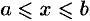 и прямыми
и прямыми 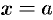 и
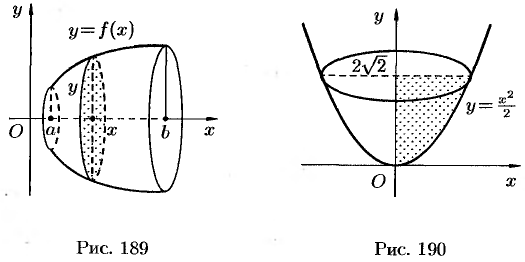
и 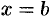 (см. рис. 189). Полученная от вращения фигура, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси
(см. рис. 189). Полученная от вращения фигура, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси  , проведенной через произвольную точку
, проведенной через произвольную точку  оси
оси  (
(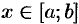 ), есть круг с радиусом
), есть круг с радиусом 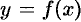 . Следовательно,
. Следовательно, 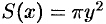 .
.
Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком непрерывной функции 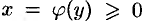 и прямыми
и прямыми 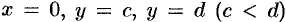 , то объем тела, образованною вращением этой трапеции вокруг оси
, то объем тела, образованною вращением этой трапеции вокруг оси 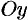 , по аналогии с формулой (41.7), равен
, по аналогии с формулой (41.7), равен

Пример №41.7.
Найти объем тела, образованною вращением фигуры, ограниченной линиями 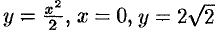 вокруг оси
вокруг оси 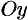 (см. рис. 190).
(см. рис. 190).
Решение:
По формуле (41.8) находим:
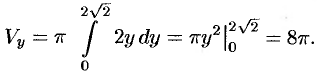
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление площадей плоских фигур |
| Вычисление длины дуги плоской кривой |
| Вычисление площади поверхности вращения |
| Работа переменной силы |

