Оглавление:
Вычисление несобственных интегралов
Несобственным интегралом называются интегралы с бесконечными пределами интегрирования и интегралы от неограниченных функций.
Рассмотрим интегралы с бесконечными пределами. Пусть функция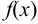 
— непрерывна при 
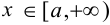. Тогда несобственный интеграл от функции 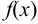в пределах от 
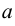до 
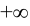определяется равенством:
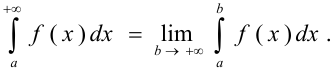
Если предел в правой части равенства существует и конечен, то несобственный интеграл называется сходящимся, если же этот предел не существует или бесконечен, то интеграл называется расходящимся.
Геометрически несобственный интеграл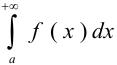 
в случае 
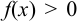представляет собой площадь фигуры, ограниченной графиком функции 
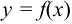, прямой 
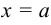и осью 
.
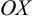Если интеграл 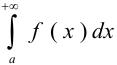сходится, то площадь фигуры выражается определённым числом, а ось 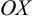служит асимптотой для графика функции 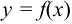. Если же интеграл 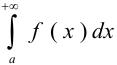расходится, то площадь фигуры бесконечна.
Аналогично вычисляется интеграл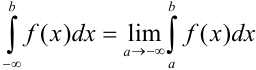 
, а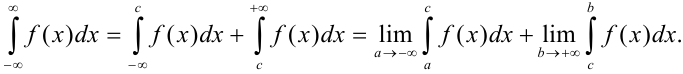 
Интеграл от неограниченной функции, т. е. если 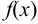непрерывна для 
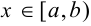и в точке 
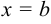имеет бесконечный разрыв, вычисляется следующим образом:
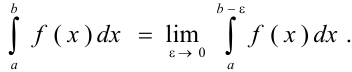
Если существует конечный предел в правой части формулы, то несобственный интеграл называется сходящимся. Аналогично
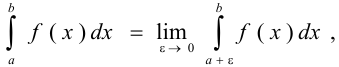
если функция 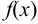имеет бесконечный разрыв в точке .
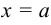Задача №96.
Вычислить несобственный интеграл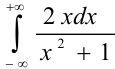 
.
Решение:
Представим данный интеграл в виде суммы:
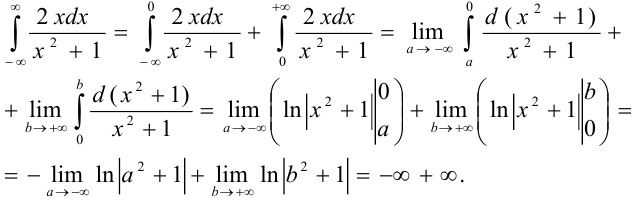
Данный интеграл расходится, так как расходится каждый из двух несобственных интегралов.
Задача №97.
Вычислить несобственный интеграл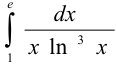 
.
Решение:
Подынтегральная функция имеет бесконечный разрыв при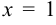 
, следовательно:
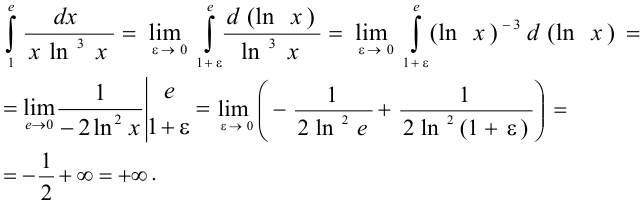
Этот интеграл расходится.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
