Оглавление:
Вычисление криволинейного интеграла II рода
Вычисление криволинейного интеграла II рода, как и I рода, может быть сведено к вычислению определенного интеграла.
Параметрическое представление кривой интегрирования
Пусть кривая 
задана параметрическими уравнениями 
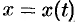и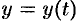 
, где функци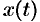и 
и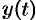 
непрерывны вместе со своими производным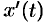и 
и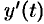 
на отрезке 
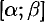, причем начальной точке 
кривой соответствует значение параметра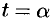 
, а конечной точке 
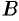— значение 
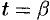. И пусть функция 
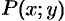непрерывна на кривой . Тогда, по определению,
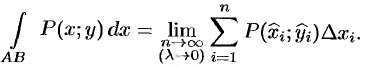
Преобразуем интегральную сумму к переменной 
. Так как
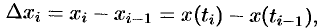
то по формуле Лагранжа (см. (25.2)) имеем: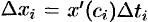 
, где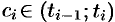 
, 
.
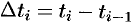Выберем точку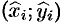 
так, чтобы 
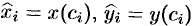. Тогда преобразованная интегральная сумма 
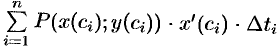будет интегральной суммой для функции одной переменной 
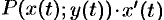на промежутке 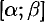. Поэтому
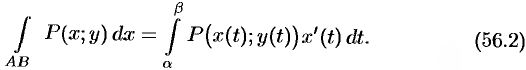
Аналогично получаем:
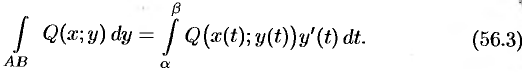
Складывая почленно полученные равенства (56.2) и (56.3), получаем:
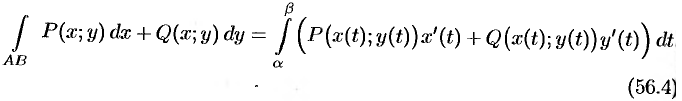
Явное представление кривой интегрирования
Если кривая задана уравнением 
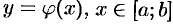, где функция и ее производная 
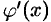непрерывны на отрезке 
, то из формулы (56.4), приняв 
за параметр, имеем параметрические уравнения кривой : 
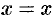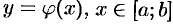, , откуда получим:
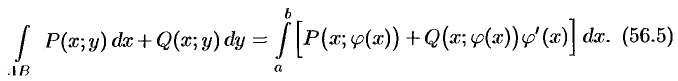
В частности,
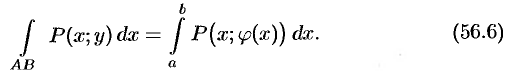
Если — гладкая пространственная кривая, которая описывается непрерывными на отрезке 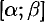функциям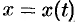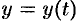и , и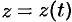 
, то криволинейный интеграл
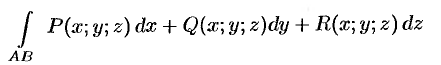
вычисляется по формуле
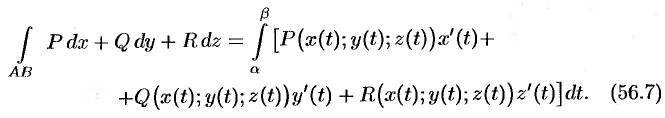
Замечание. Криволинейные интегралы I и II рода связаны соотношением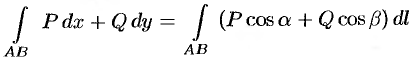 
, где 
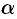и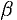 
— углы, образованные касательной к кривой в точке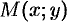 
с осями 
и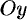 
соответственно.
Пример №56.1.
Вычислить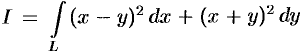 
, 
—
ломаная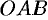 
, где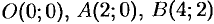 
.
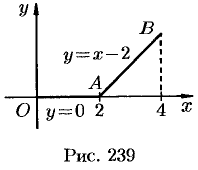
Решение:
Так как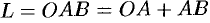 
(см. рис. 239), то 
.
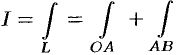Уравнение отрезка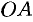 
есть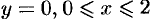 
; уравнение отрезка : 
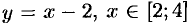. Согласно формуле (56.5), имеем:
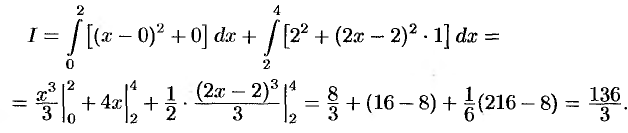
Пример №56.2.
Вычислить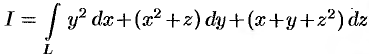 
, — отрезок прямой в пространстве от точки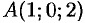 
до точки 
.
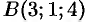Решение:
Составим уравнение прямой, проходящей через точки и :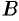 
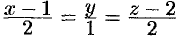или в параметрической форме: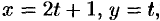 
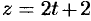. При перемещении от точки к точке 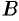параметр меняется от 0 до 1. По формуле (56.7) находим, что
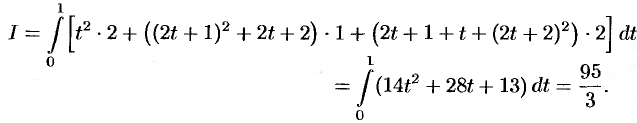
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
