Вычисление главного вектора и главного момента произвольной пространственной системы сил
Главным вектором 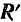 любой системы сил называется геометрическая сумма всех сил системы.
любой системы сил называется геометрическая сумма всех сил системы.
Проектируя все силы данной пространственной системы сил на три взаимно перпендикулярные оси, мы можем найти модуль и направление главного вектора этой системы по формулам (8):
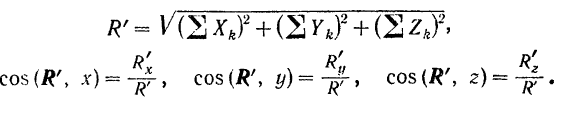
Главным моментом 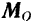 пространственной системы сил относительно какой-либо точки
пространственной системы сил относительно какой-либо точки 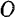 называется (см. стр. 71) геометрическая сумма моментов всех сил системы относительно этой точки
называется (см. стр. 71) геометрическая сумма моментов всех сил системы относительно этой точки
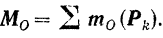
Для того чтобы найти главный момент пространственной системы сил относительно точки 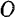 , надо построить согласно установленному ранее правилу (стр. 67) моменты этих сил, а затем сложить их по правилу векторного многоугольника. Замыкающая сторона многоугольника и будет представлять собой искомый главный момент.
, надо построить согласно установленному ранее правилу (стр. 67) моменты этих сил, а затем сложить их по правилу векторного многоугольника. Замыкающая сторона многоугольника и будет представлять собой искомый главный момент.
Подобная, принципиально простая, геометрическая операция для нахождения главного момента пространственной системы сил требует громоздких пространственных построений и практически, конечно, малоудобна. Значительно проще определить главный момент относительно какой-либо точки 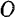 , приняв эту точку за начало координат и определив моменты всех сил данной системы относительно трех любых взаимно перпендикулярных осей, проходящих через эту точку.
, приняв эту точку за начало координат и определив моменты всех сил данной системы относительно трех любых взаимно перпендикулярных осей, проходящих через эту точку.
Проекция геометрической суммы моментов на любую ось равна алгебраической сумме проекций на ту же ось составляющих векторов. Но проекция момента силы относительно точки на какую-либо ось, проходящую через эту точку, есть момент силы относительно этой оси.
Следовательно, обозначая проекции гласного момента 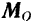 на соответствующие координатные оси через
на соответствующие координатные оси через
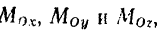
будем иметь:
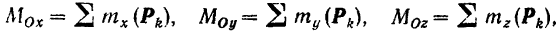
где
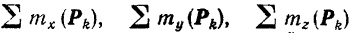
алгебраические суммы моментов всех сил данной системы относительно соответствующих координатных осей.
Зная же проекции вектора на три взаимно перпендикулярные оси, легко найти как его модуль, так и его направление, пользуясь общими зависимостями между вектором и его проекциями на оси (формулы (4) и (5)). Модуль главного момента
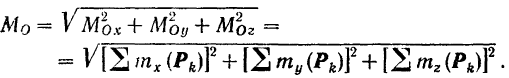
Направляющие косинусы
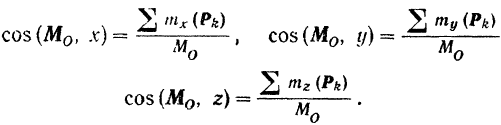
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

