Вычисление главного вектора и главного момента произвольной плоской системы сил
В § 20 было показано, что любая система сил эквивалентна по своему действию на абсолютно твердое тело совокупности: одной силы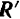 
, равной главному вектору данной системы сил, приложенной с произвольно выбранной точке тела (в центре приведения), и одной пары, момент которой равен главному моменту 
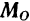данной системы сил относительно выбранного центра 
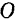приведения.
Главный вектор 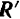любой системы сил равен, как известно, геометрической сумме всех сил данной системы.
Для плоской системы сил модуль и направление главного вектора вычисляются аналитически по формулам (8):
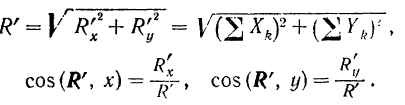
В общем случае произвольной пространственной системы сил главный момент ее относительно какой-либо точки равен геометрической сумме моментов всех сил системы относительно этой точки.
В частном же случае, когда все силы лежат в одной плоскости, момент силы относительно точки можно рассматривать (§21) как скалярную величину, и потому главный момент плоской системы сил относительно любой точки , лежащей в плоскости действия сил, равен сумме алгебраических величин моментов всех сил системы относительно той же точки:
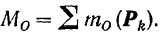
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
