Оглавление:
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных  и
и  (замену переменных) как
(замену переменных) как
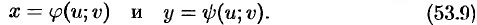
Если функции (53.9) имеют в некоторой области  плоскости
плоскости  не прерывные частные производные первого порядка и отличный от нуля определитель
не прерывные частные производные первого порядка и отличный от нуля определитель
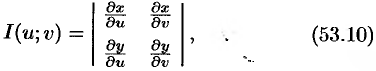
а функция 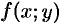 непрерывна в области
непрерывна в области  , то справедлива формула замены переменных в двойном интеграле:
, то справедлива формула замены переменных в двойном интеграле:
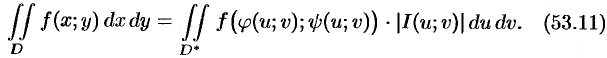
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат  и
и  полярными координатами
полярными координатами 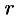 и
и 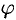 .
.
В качестве 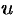 и
и 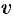 возьмем полярные координаты
возьмем полярные координаты 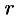 и
и 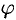 . Они связаны с декартовыми координатами формулами
. Они связаны с декартовыми координатами формулами 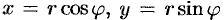 (см п. 9.1).
(см п. 9.1).
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
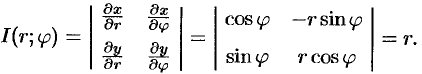
Формула замены переменных (53.11) принимает вид:
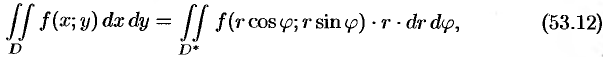
где 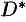 — область в полярной системе координат, соответствующая области
— область в полярной системе координат, соответствующая области  в декартовой системе координат.
в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область 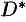 имеет вид, изображенный на рисунке 221 (ограничена лучами
имеет вид, изображенный на рисунке 221 (ограничена лучами 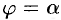 и
и 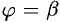 , где
, где 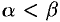 , и кривыми
, и кривыми 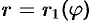 и
и 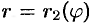 , где
, где 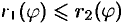 , т. е. область
, т. е. область 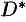 правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
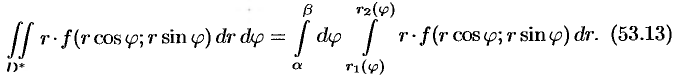
Внутренний интеграл берется при постоянном 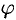 .
.
Замечания.
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
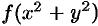 , область
, область  есть круг, кольцо или часть таковых.
есть круг, кольцо или часть таковых. - На практике переход к полярным координатам осуществляется путем замены
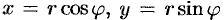 ,
, 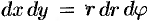 ; уравнения линий, ограничивающих область
; уравнения линий, ограничивающих область  , также преобразуются к полярным координатам. Преобразование области
, также преобразуются к полярным координатам. Преобразование области  в область
в область 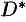 не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 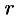 и
и 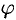 (исследуя закон изменения
(исследуя закон изменения 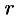 и
и 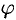 точки
точки 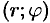 при ее отождествлении с точкой
при ее отождествлении с точкой 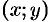 области
области  ).
).
Пример №53.2.
Вычислить 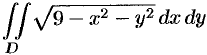 , где область
, где область  — круг
— круг 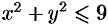 .
.
Решение:
Применив формулу (53.12), перейдем к полярным координатам:
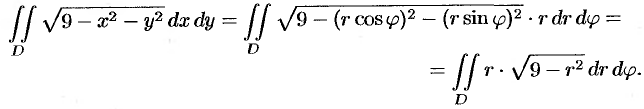
Область  в полярной системе координат определяется неравенствами (см. рис. 222)
в полярной системе координат определяется неравенствами (см. рис. 222) 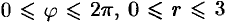 . Заметим: область
. Заметим: область  — круг — преобразуется в область
— круг — преобразуется в область  — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
— прямоугольник. Поэтому, согласно формуле (53.13), имеем:
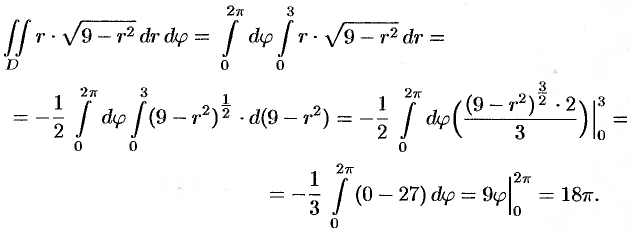
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Масса плоской пластинки |
| Вычисление двойного интеграла в декартовых координатах |
| Приложения двойного интеграла |
| Вычисление тройного интеграла в декартовых координатах |

