Оглавление:
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 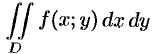 , где функция
, где функция 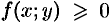 непрерывна в области
непрерывна в области  . Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью
. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью  . Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
. Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
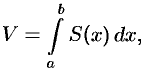
где 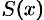 — площадь сечения плоскостью, перпендикулярной оси
— площадь сечения плоскостью, перпендикулярной оси  , а
, а 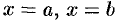 — уравнения плоскостей, ограничивающих данное тело.
— уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми  и
и  и кривыми
и кривыми 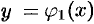 и
и 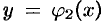 , причем функции
, причем функции 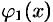 и
и 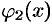 непрерывны и таковы, что
непрерывны и таковы, что 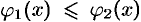 для всех
для всех 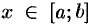 (см. рис. 218). Такая область называется правильной в направлении оси
(см. рис. 218). Такая область называется правильной в направлении оси 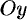 : любая прямая, параллельная оси
: любая прямая, параллельная оси 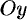 , пересекает границу области не более чем в двух точках.
, пересекает границу области не более чем в двух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси 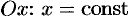 , где
, где 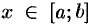 .
.
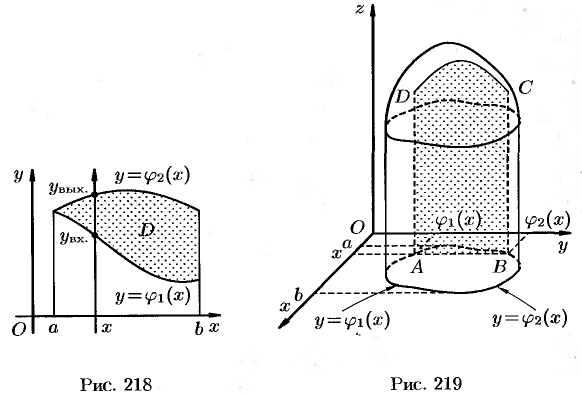
В сечении получим криволинейную трапецию 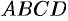 , ограниченную линиями
, ограниченную линиями  , где
, где 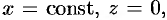
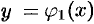 и
и 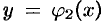 (см. рис. 219).
(см. рис. 219).
Площадь 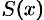 этой трапеции находим с помощью определенного интеграла
этой трапеции находим с помощью определенного интеграла
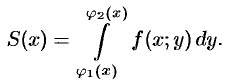
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
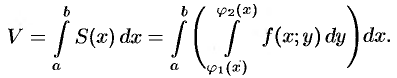
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 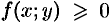 по области
по области  . Следовательно,
. Следовательно,
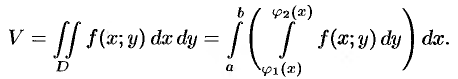
Это равенство обычно записывается в виде
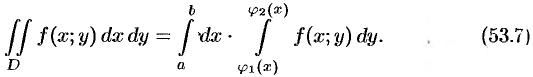
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции 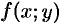 по области
по области  . При этом
. При этом  называется внутренним, интегралом.
называется внутренним, интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая  постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по
постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по  в пределах от
в пределах от 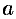 до
до 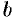 .
.
Если же область  ограничена прямыми
ограничена прямыми 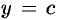 и
и 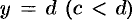 , кривыми
, кривыми 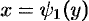 и
и 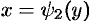 , причем
, причем 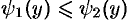 для всех
для всех 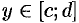 , т. е. область
, т. е. область  — правильная в направлении оси
— правильная в направлении оси  , то, рассекая тело плоскостью
, то, рассекая тело плоскостью 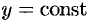 , аналогично получим:
, аналогично получим:
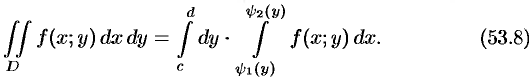
Здесь, при вычислении внутреннего интеграла, считаем  постоянным.
постоянным.
Замечания.
- Формулы (53.7) и (53.8) справедливы и в случае, когда
 ,
, 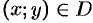 .
. - Если область
 правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8). - Если область
 не является правильной ни «по
не является правильной ни «по  », ни «по
», ни «по  », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси
», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси  или оси
или оси 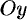 .
. - Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример №53.1.
Вычислить 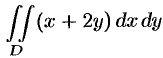 , где область
, где область  ограничена линиями
ограничена линиями  .
.
Решение:
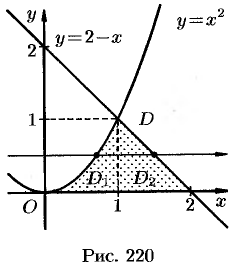
На рисунке 220 изображена область интегрирования  . Она правильная в направлении оси
. Она правильная в направлении оси  . Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
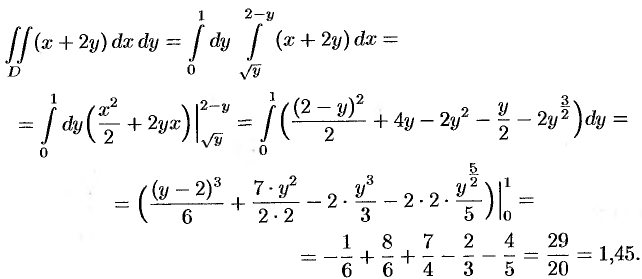
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область  следует разбить на две области:
следует разбить на две области: 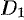 и
и 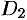 . Получаем:
. Получаем:
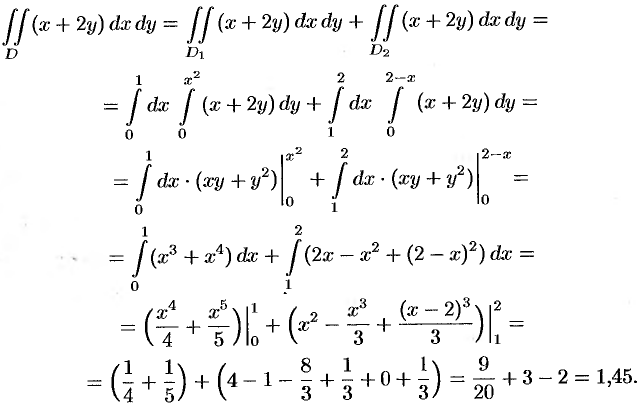
Ответ, разумеется, один и тот же.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Объем цилиндрического тела |
| Масса плоской пластинки |
| Вычисление двойного интеграла в полярных координатах |
| Приложения двойного интеграла |

