Оглавление:
Рассмотрим функцию 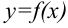 , непрерывную на отрезке
, непрерывную на отрезке 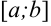 . С помощью метода сумм (лекция 21) выводятся две важные формулы:
. С помощью метода сумм (лекция 21) выводятся две важные формулы:
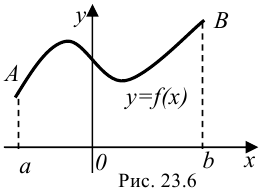
1. Длина дуги 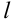 кривой
кривой 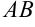 , заданной на отрезке
, заданной на отрезке 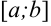 (рис. 23.6) при условии непрерывности
(рис. 23.6) при условии непрерывности 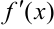 , выражается формулой:
, выражается формулой: 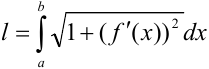 .
.
Пример №23.3.
Найдите длину дуги линии 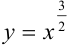 от точки
от точки 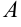 (0; 0) до точки
(0; 0) до точки 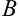 (1; 1).
(1; 1).
Решение:
Для вычисления длины дуги 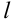 воспользуемся формулой:
воспользуемся формулой: 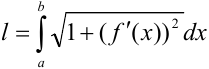 .
.
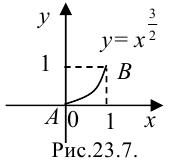
В качестве  берем функцию
берем функцию 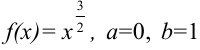 (рис. 23.7). Тогда
(рис. 23.7). Тогда 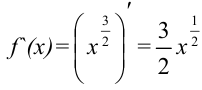 , и
, и 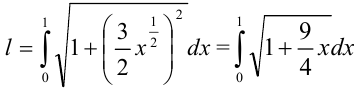 . Представим квадратный корень в виде степени:
. Представим квадратный корень в виде степени: 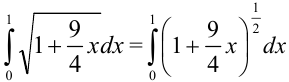 . Вычислим данный интеграла как интеграл от некоторой сложной функции:
. Вычислим данный интеграла как интеграл от некоторой сложной функции: 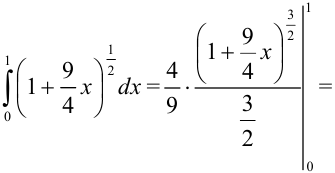
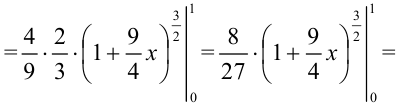
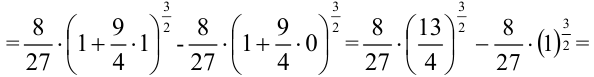
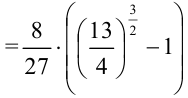
Ответ: 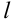
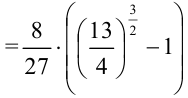 .
.
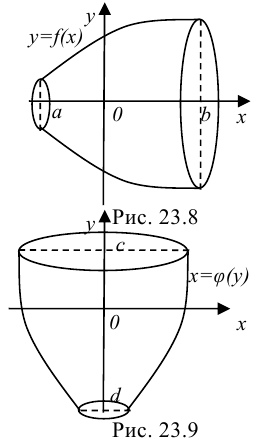
2. Объем тела вращения, полученного вращением вокруг оси 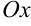 криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции 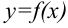 , отрезком
, отрезком 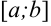 , прямыми
, прямыми 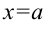 и
и 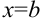 (рис. 23.8), выражается формулой:
(рис. 23.8), выражается формулой: 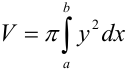 .
.
Объем тела вращения, полученного вращением вокруг оси 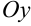 криволинейной трапеции, ограниченной графиком непрерывной функции
криволинейной трапеции, ограниченной графиком непрерывной функции 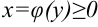 , прямыми
, прямыми 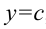 ,
, 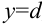 ,
, 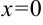 (рис. 23.9), выражается формулой:
(рис. 23.9), выражается формулой: 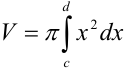 .
.
Пример №23.4.
Найдите объем тела, полученного вращением вокруг оси 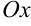 фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции 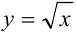 , осью
, осью 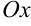 , прямой
, прямой 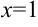 .
.
Решение:
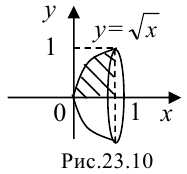
Построим фигуру, ограниченную графиком функции 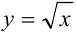 , осью
, осью 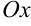 , прямой
, прямой 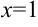 (на рис. 23.10 обозначена штриховкой). При ее вращении вокруг оси
(на рис. 23.10 обозначена штриховкой). При ее вращении вокруг оси 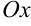 получаем тело вращения (рис. 23.10). Для вычисления его объема воспользуемся формулой:
получаем тело вращения (рис. 23.10). Для вычисления его объема воспользуемся формулой: 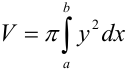 .
.
В нашем примере 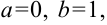
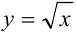 . Тогда
. Тогда 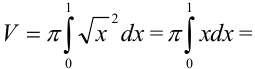
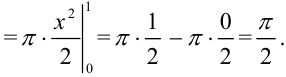
Ответ: 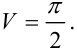
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Геометрический смысл определенного интеграла |
| Приложение определенного интеграла к вычислению площадей плоских фигур. |
| Понятие несобственного интеграла |
| Несобственные интегралы I рода. |

