Оглавление:
Вычисление длины дуги плоской кривой
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая 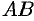 , уравнение которой
, уравнение которой  , где
, где 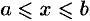 .
.
Под длиной дуги 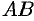 понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю.
понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю.
Покажем, что если функция  и ее производная
и ее производная 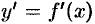 непрерывны на отрезке
непрерывны на отрезке  , то кривая
, то кривая 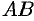 имеет длину, равную
имеет длину, равную
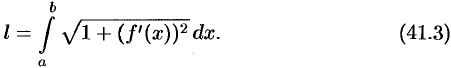
Применим схему I (метод сумм).
1. Точками 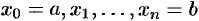
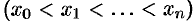 разобьем отрезок
разобьем отрезок  на
на  частей (см. рис. 182). Пусть этим точкам соответствуют точки
частей (см. рис. 182). Пусть этим точкам соответствуют точки 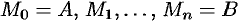 на кривой
на кривой 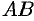 . Проведем хорды
. Проведем хорды 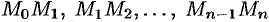 , длины которых обозначим соответственно через
, длины которых обозначим соответственно через 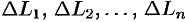 . Получим ломаную
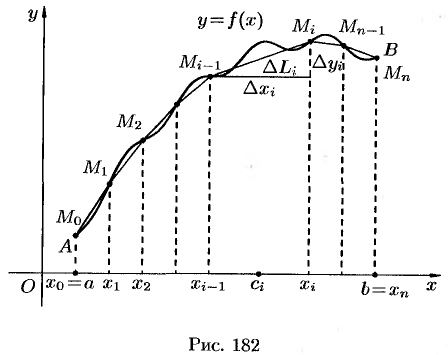
. Получим ломаную  длина которой равна
длина которой равна 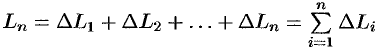 .
.
2. Длину хорды (или звена ломаной) 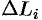 можно найти по теореме Пифагора из треугольника, с катетами
можно найти по теореме Пифагора из треугольника, с катетами 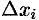 и
и 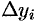 :
:
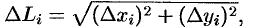
где 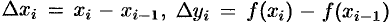 . По теореме Лагранжа о конечном приращении функции
. По теореме Лагранжа о конечном приращении функции 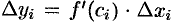 , где
, где 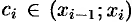 . Поэтому
. Поэтому
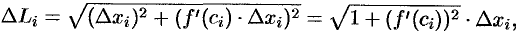
а длина всей ломаной 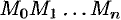 равна
равна
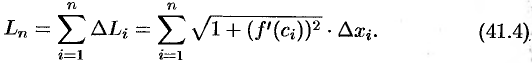
3. Длина 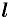 кривой
кривой 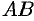 , но определению, равна
, но определению, равна
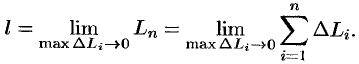
Заметим, что при 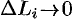 также и
также и 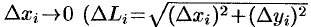 и, следовательно,
и, следовательно, 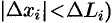 . Функция
. Функция 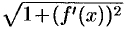 непрерывна на отрезке
непрерывна на отрезке  , так как, по условию, непрерывна функция
, так как, по условию, непрерывна функция 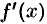 . Следовательно, существует предел интегральной суммы (41.4), когда
. Следовательно, существует предел интегральной суммы (41.4), когда 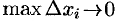 :
:
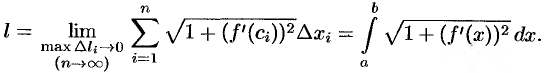
Таким образом, 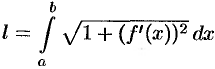 , или в сокращенной записи
, или в сокращенной записи 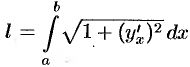 .
.
Если уравнение кривой 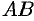 задано в параметрической форме
задано в параметрической форме
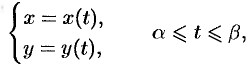
где 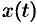 и
и 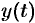 — непрерывные функции с непрерывными производными и
— непрерывные функции с непрерывными производными и 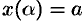 ,
, 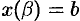 , то длина
, то длина 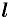 кривой
кривой 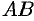 находится по формуле
находится по формуле
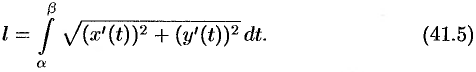
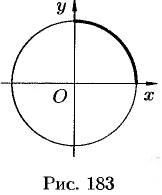
Формула (41.5) может быть получена из формулы (41.3) подстановкой 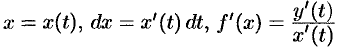 .
.
Пример №41.4.
Найти длину окружности радиуса 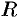 .
.
Решение:
Найдем 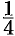 часть ее длины от точки
часть ее длины от точки 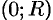 до точки
до точки 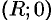 (см. рис. 183). Так как
(см. рис. 183). Так как 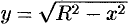 , то
, то
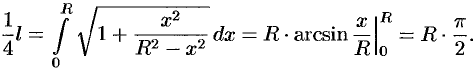
Значит, 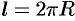 . Если уравнение окружности записать в параметрическом виде
. Если уравнение окружности записать в параметрическом виде 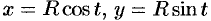
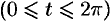 , то
, то
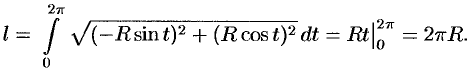
Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).
1. Возьмем произвольное значение 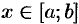 и рассмотрим переменный отрезок
и рассмотрим переменный отрезок 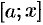 . На нем величина
. На нем величина 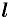 становится функцией от
становится функцией от  , т. е.
, т. е. 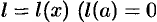 и
и 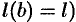 .
.
2. Находим дифференциал 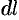 функции
функции 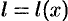 при изменении
при изменении  на малую величину
на малую величину 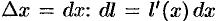 . Найдем
. Найдем 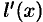 , заменяя бесконечно малую дугу
, заменяя бесконечно малую дугу 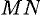 хордой
хордой 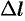 , стягивающей эту дугу (см. рис. 184):
, стягивающей эту дугу (см. рис. 184):
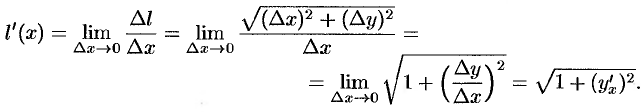
Стало быть, 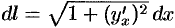 .
.
3. Интегрируя 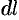 в пределах от
в пределах от 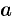 до
до 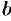 , получаем
, получаем 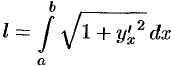 .
.
Равенство 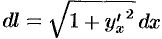 называется формулой дифференциала дуги в прямоугольных координатах.
называется формулой дифференциала дуги в прямоугольных координатах.
Так как 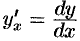 , то
, то
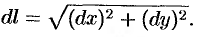
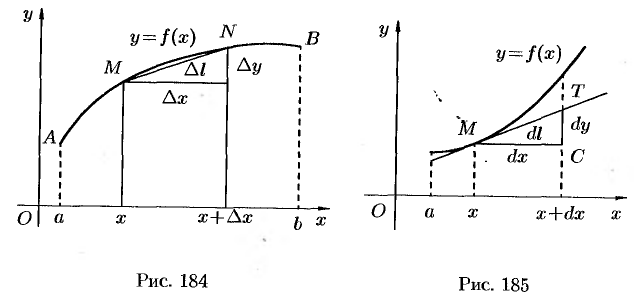
Последняя формула представляет собой теорему Пифагора для бесконечно малого треугольника 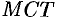 (см. рис. 185).
(см. рис. 185).
Полярные координаты
Пусть кривая 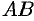 задана уравнением в полярных координатах
задана уравнением в полярных координатах 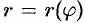 ,
, 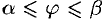 . Предположим, что
. Предположим, что 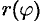 и
и 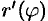 непрерывны на отрезке
непрерывны на отрезке 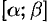 .
.
Если в равенствах 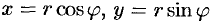 , связывающих полярные и декартовы координаты, параметром считать угол
, связывающих полярные и декартовы координаты, параметром считать угол 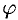 , то кривую
, то кривую 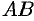
можно задать параметрически 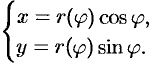 Тогда
Тогда
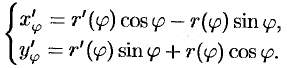
Поэтому
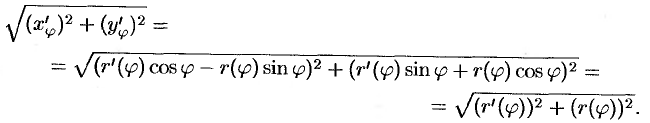
Применяя формулу (41.5), получаем
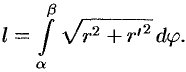
Пример №41.5.
Найти длину кардиоиды 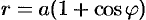 .
.
Решение:
Кардиоида 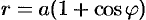 имеет вид, изображенный на рисунке 186. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:
имеет вид, изображенный на рисунке 186. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:
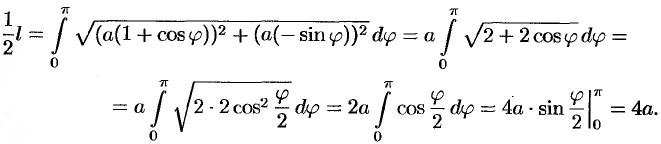
Таким образом, 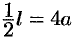 . Значит,
. Значит, 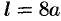 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Схемы применения определенного интеграла |
| Вычисление площадей плоских фигур |
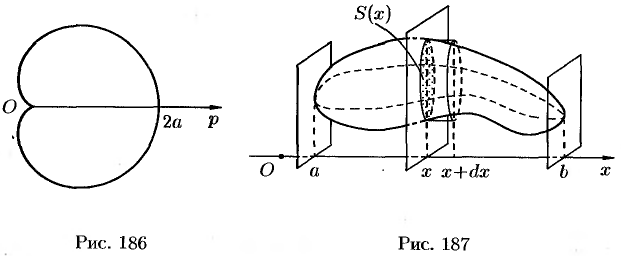
| Вычисление объема тела |
| Вычисление площади поверхности вращения |

