Понятие вычета и основная теорема о вычетах
Вычетом аналитической функции 
в изолированной особой точке 
называется комплексное число, равное значению интеграла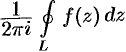 
, взятого в положительном направлении по окружности 
с центром в точке , лежащей в области аналитичности функции (т. е. в кольце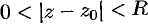 
).
Обозначается вычет функции в изолированной особой точке символом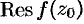 
или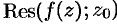 
. Таким образом,
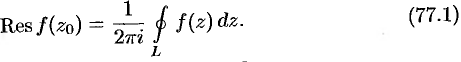
Если в формуле (76.12) положить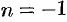 
, то получим
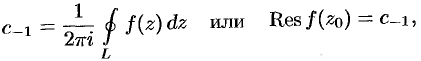
т. е. вычет функции относительно особой точки равен коэффициенту при первом члене с отрицательным показателем в разложении функции в ряд Лорана (76.11).
Теорема 77.1 (Коши). Если функция является аналитической в замкнутой области 
, ограниченной контуром , за исключением конечного числа особых точек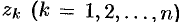 
, лежащих внутри области 
, то
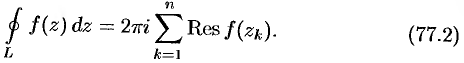
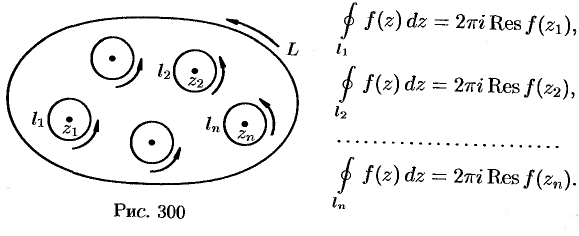
Вокруг каждой особой точки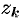 
опишем окружность 
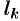так, чтобы она целиком содержалась в области , не содержала внутри других особых точек и чтобы никакие две из этих окружностей не имели общих точек (см. рис. 300).
Тогда на основании теоремы Коши для многосвязной области (см. замечание на с. 545) имеем:
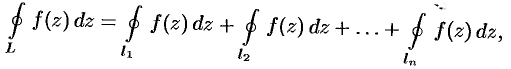
где при интегрировании все контуры обходятся против часовой стрелки. Но, согласно формуле (77.1), имеем:
Следовательно,
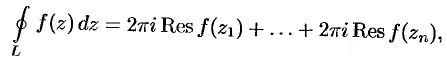
т.е.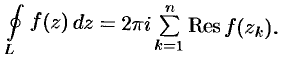 
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Основные элементарные функции комплексного переменного |
| Ряды в комплексной плоскости |
| Преобразование Лапласа |
| Операционный метод решения линейных дифференциальных уравнений и их систем |
