Оглавление:
Выбор функции тренда
Самым распространенным методом моделирования тенденции динамического ряда является аналитическое выравнивание. Аналитическое выравнивание динамического ряда состоит в выражении тенденции развития в виде функции изучаемого показателя от времени, называемой моделью тренда. Функции, описывающие закономерности развития явлений во времени, называют кривыми роста.
В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда — как функция этой независимой переменной. При этом следует подчеркнуть, что развитие явления во времени рассматривается как результат действия факторов, влияющих на это развитие.
Существуют различные приемы, позволяющие выбирать тип кривой, достаточно хорошо аппроксимирующей тенденцию. Наиболее простой способ состоит в выборе функции на основе графического изображения временного ряда.
Второй способ выбора типа кривой заключается в применении метода последовательных разностей.
Тип кривой можно выбрать и на основании значения суммы квадратов отклонений, заданных уровней динамического ряда от расчетных, полученных выравниванием.
Наиболее приемлемым является метод, основанный на сравнении характеристик изменения приростов исследуемого динамического ряда и соответствующих характеристик кривых роста. Для сглаживания выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения уровней динамического ряда. Этот метод называется методом характеристик прироста. Для применения метода характеристик прироста:
• проводят сглаживание динамического ряда скользящей средней;
• определяют средние значения приростов;
• вычисляют характеристики прироста:
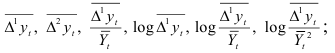
• выбирают тип кривой.
Сглаживание динамического ряда скользящей средней по формулам (3.5), (3.12) (см. [l]) дает возможность определить тенденцию изменения ряда.
При вычислении взвешенных скользящих средних приростов применяют рекуррентные формулы:
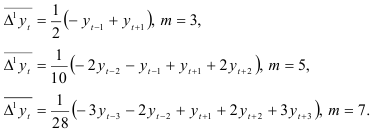
Вычислив средние приросты динамического ряда, определяют ряд производных характеристик прироста. Анализируя изменение средних приростов и их характеристик, сравнивают их с соответствующими характеристиками кривых роста (табл. 7.2).


В тех случаях, когда значения средних приростов 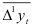 оказываются отрицательными, рекомендуется увеличить интервал усреднения, принятый для вычисления скользящей средней, или заменить уровни динамического ряда, для которых получаются отрицательные
оказываются отрицательными, рекомендуется увеличить интервал усреднения, принятый для вычисления скользящей средней, или заменить уровни динамического ряда, для которых получаются отрицательные 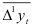 , расчетными величинами, например средними из уровней, предшествующих таким уровням и следующих за ними (достаточно взять по два уровня до и после момента t).
, расчетными величинами, например средними из уровней, предшествующих таким уровням и следующих за ними (достаточно взять по два уровня до и после момента t).
Если исследуемый динамический ряд имеет понижающуюся тенденцию, то средние приросты вычисляют в обратном направлении, т.е. с конца ряда.
Для подбора типа кривой можно воспользоваться также рекомендациями, изложенными ниже.
Пример 7. 2.
Производство ткани (млн. м2) в Беларуси характеризуются динамическим рядом, представленным в табл. 7.3 (первый и второй столбцы).
Для выбора формы кривой вычислим конечные разности и характеристики приростов исследуемого динамического ряда. Результаты вычислений сведены в таблице 7.3. Как видим из третьего, четвертого и пятого столбцов таблицы 7.3, конечные разности заметно варьируют. Следовательно, полиномы первой, второй, третьей и более высоких степеней не подходят в качестве кривых, описывающих тренд динамического ряда. Поэтому применим метод характеристик приростов. Для этого проведем сглаживание ряда семилетней скользящей средней (шестой столбец), которое дает возможность наметить тенденцию изменения уровней ряда. Определим средние приросты по формуле:
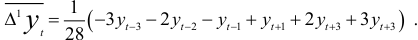
Вычислим характеристики приростов:
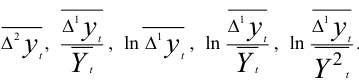
В таблице 7.3 приведены значения средних приростов и их характеристик, анализ которых показывает, что отношение 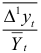 , примерно одинаковые. Следовательно, в качестве кривой тренда можно выбрать экспоненциальную функцию
, примерно одинаковые. Следовательно, в качестве кривой тренда можно выбрать экспоненциальную функцию
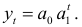
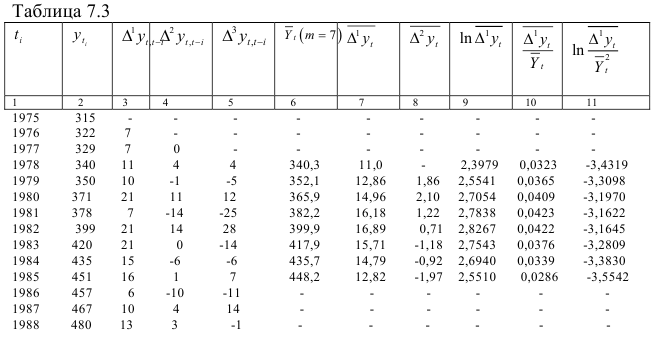
Пример 7.3.
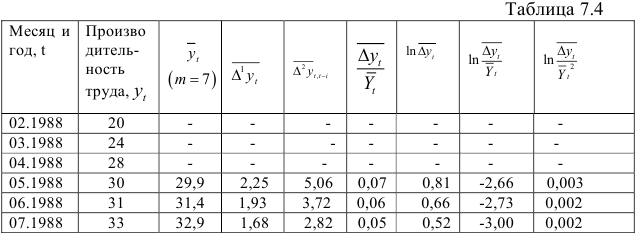
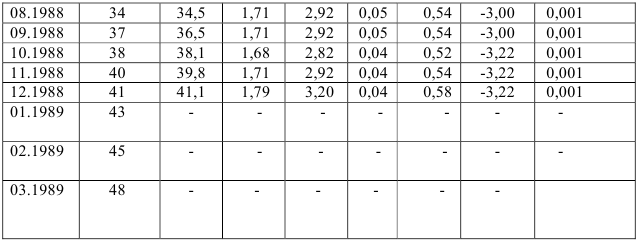
Введение механизации на предприятии позволило увеличить производительность труда. С февраля 1988г по апрель 1989г производительность характеризуется динамическим рядом, представленным в табл. 7.4, (первый и второй столбцы).
Семилетнюю скользящую среднюю вычислим по формуле:
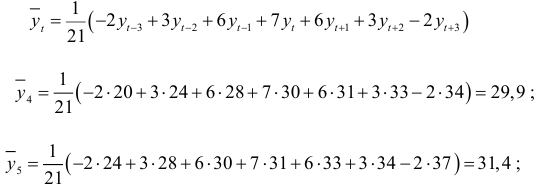
и т.д. Анализируя значения семилетней скользящей средней, можно сделать вывод о том, что тенденция приближается к линейной.
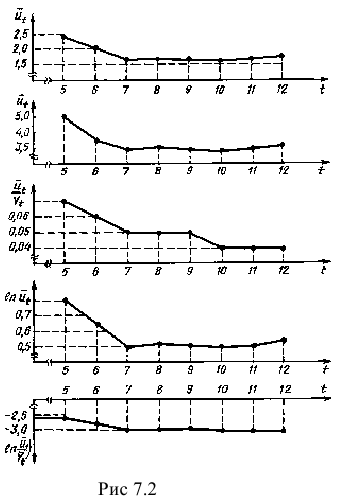
Для проверки этого вывода вычислим характеристики приростов (см. табл. 7.4) и построим соответствующие графики (рис. 7.2). Средние приросты вычислим, используя формулу:
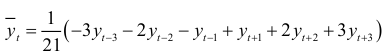
Анализ значений характеристик приростов и их графиков подтверждает сделанное предположение о том, что тенденция динамического ряда описывается линейной функцией:
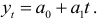
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Моделирование одномерных временных рядов |
| Агрегатная модель компонент уровня ряда динамики |
| Методы определения сезонных колебаний |
| Анализ и моделирование случайной компоненты |

