Оглавление:




Вычисление углового ускорения
- Чтобы рассчитать ускорение точки тела, вам нужно знать угловое ускорение e. Рассмотрим два основных способа его расчета. 1. Если проекция угловой скорости <о, „на подвижную или фиксированную ось координаты Го известна, проекция углового ускорения на ту же ось определяется по следующей формуле. £ x = do) x / dr; eJ, = do ,, / df; £ z = da> 2 / dz. (16) Из проекции вы можете легко найти косинус угла между коэффициентом углового ускорения и осью координат. 2.
Поэтому, каким бы ни был гул в первый момент, он стремится к одному и тому же пределу K,и через достаточно долгое время движение становится почти равномерным со скоростью K. Людмила Фирмаль
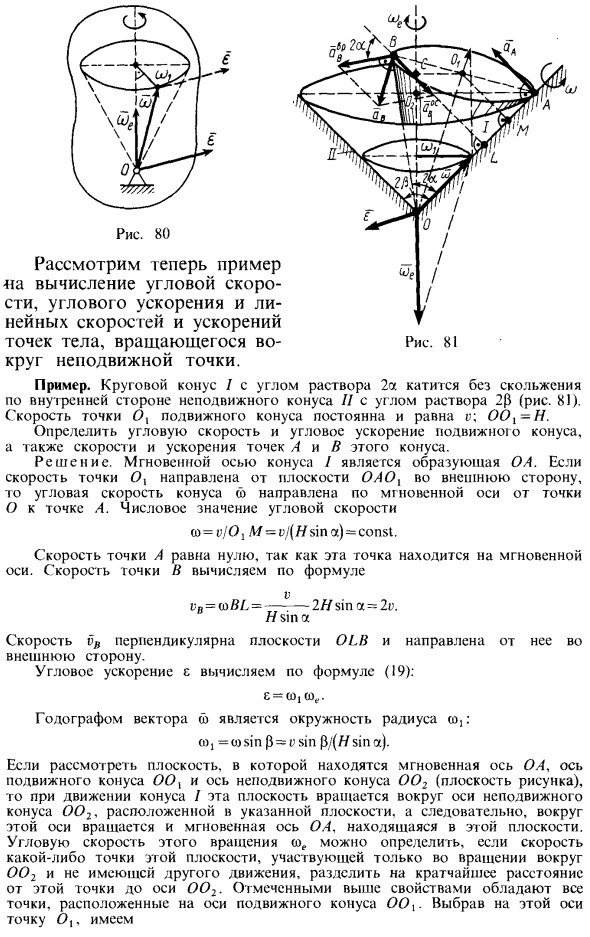
Другой способ определения углового ускорения основан на разложении на две взаимно перпендикулярные составляющие. Введя единичный вектор a> °, ориентированный вдоль r, д = <о °; e = da / di = (d 0+ 0, направление идет вдоль вектора d, и наоборот, если dco / dr _ Раствор 2a j_____ катится под углом Раствора 2p без скольжения вдоль внутренней части неподвижного конуса II (Рис. 8)). Точка скорости O | Конус качения постоянен и равен o. O0 = H. Определите угловую скорость и ускорение движущегося конуса, а также скорость и ускорение точек A и B этого конуса. Решения.
- Мгновенная ось конуса / представляет собой шину OA. Если скорость в точке O направлена наружу от плоскости компании, угловая скорость конуса направлена из точки O в точку A вдоль мгновенной оси. Числовое значение угловой скорости Поскольку эта точка находится на мгновенной оси, скорость точки A равна нулю. Скорость точки B рассчитывается по следующей формуле Формула (19): Внешняя скорость. Угловое ускорение Годографом вектора r является окружность с радиусом ω: o> 1 = oJsinp = t, sinp / (// sina). Рассмотрим плоскость, где расположена мгновенная ось OA.
В этих случаях, как и при трении во время движения, как и при трении в начале движения, возникают какие-то особые обстоятельства, которые могут привести либо к неопределенности, либо к невозможности выполнения поставленной задачи. Людмила Фирмаль
Когда ось подвижного конуса OO, ось неподвижного конуса 002 (плоскость на фигуре) и конус I перемещаются, эта плоскость вращается вокруг оси неподвижного конуса OO2. Поскольку он находится в указанной плоскости, он вращается вокруг этой оси и становится мгновенной осью OA. В этом самолете. Угловая скорость этого вращения Помните, что вы получите. Угловая скорость На мгновенной оси. n <Развернуть параллелограммную вилку вала Мобильный и стационарный конус. Тогда компонентом вдоль оси неподвижного конуса является угловая скорость d.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

