Вычисление статических моментов и центра тяжести кривой

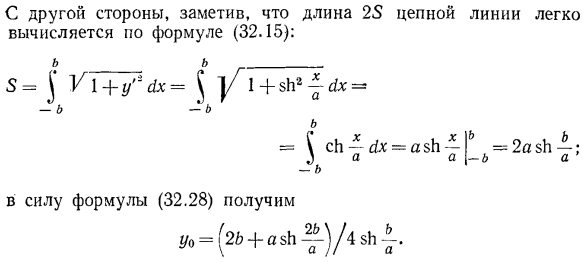
Вычисление статических моментов и центра тяжести кривой

Вычисление статических моментов и центра тяжести кривой. Пусть M-материальная точка массовой точки m с координатами x и y. рабочие моменты tu и tx называются моментами относительно осей Ox и Oy соответственно. Пусть Γ= {r (e), 0 5 5} фиксируемая кривая. Пять Переменная длина дуги. Предположим, что кривая Γ имеет массу, и масса этой дуги прямо пропорциональна длине дуги. Если Am-масса дуги длины Dk, то Am = pD5, где p-константа, называемая линейной плотностью кривой G. Кривые динамики называются однородными. Р =-^、 Плотность равна массе длины дуги кривой на единицу длины дуги. Для простоты предположим, что масса части кривой p = 1, то есть длина De, также равна D, в частности, масса всей кривой численно равна. 32.6.

Все фундаментальные моменты, которые стремятся к нулю в тонкости разбиения m, называются моментами кривой для оси Ox (Oy). Людмила Фирмаль

• Расчет статического момента центроида кривой 509 Где m = {5, -}?{5-разбиение отрезка [0, 5], Az-C. −3; -!Янки 1-1, 2, во втором иннинге… k. разбиение m соответствует разбиению,= {r (5), 5y = ^ 5 ^ 5.} на участок кривой Γ Γ.At в какой-то точке выберите e [5 (_5.]) и поставьте x,= x ( | , -), y,= y {{), 1 = 1, 2k. Значение VgA3 называется базовым статическим моментом частичного Гг кривой г относительно оси Ox, если выбрана указанная точка. Очевидно, что основной статический момент ГI численно равен моменту ординатной точки Ae, то есть эта непрерывная кривая Tk заменяется точкой точки AE. Определение 3.Пределы, которые ищет сумма 2 У1 Л5; (32.25） 1 = 1.

По определению кривой, функция r = r (s), а следовательно, координатная функция x = x(s), y = y (5) непрерывна на интервале[0, 5], поэтому это ограничение всегда присутствует. Поскольку сумма(32.25) является интегральной суммой Римана функции y (s), Если b » 0 Пять Интеграция имеет тенденцию быть^ y (s) c1z. как это О Пять МХ ^мудрый. (32.26） Да. Аналогично определяется и вычисляется момент M кривой Γ для оси Ox. Восемь Му = \ ху&. (32.27） О Определение 4.Точка плоскости P =(x0, y0). Это называется центроидом кривой, где если поставить точку массы, равную массе кривой (если рассматривается масса 8), то эта точка будет иметь статический момент относительно любой координатной оси, равный статическому моменту кривой вокруг той же оси.

• Подобный этому 5×0 = му, 8y0 = МХ. Отсюда уравнение центроидных координат (32.26) и (32.27) дает уравнение§ 32.Геометрическое и физическое применение интегралов Пятьсот десять Сравните формулу для ординаты центроида кривой Пять y08 = \ yl1z и площадь поверхности B, полученная из счетчика Пять Когда эта кривая вращается вокруг определенной оси b = 2n \ yy, она выглядит так. Шесть Интересным соотношением L-2L03 (где кривая означает непрерывно дифференцируемую кривую без сингулярности) является содержание так называемой первой теоремы Гульдина a*’. Теорема 5 (Гульдин).

Площадь поверхности, полученная в результате вращения кривой вокруг непересекающейся оси, равна произведению окружности, описываемой длиной этой кривой, и центроида этой кривой. Например, площадь поверхности, полученная при вращении вокруг оси Oy в окружности (x-a) 2 + y2 = r2, 0 g a(такая поверхность называется Тором), может быть легко вычислена этим методом. / , = 2размера-2lg = 4a2ag. Это связано с тем, что центр тяжести круга совпадает с его центром. В качестве примера вычисления центроида кривой Для Формулы (32.28) центроид цепной линии y = A cb ^-、 b ^ x ^ b. симметрия цепной линии относительно оси Oy делает Mu = 0.In факт, если вы выберете точку цепной линии на оси Oy в начале дуги и укажете длину всей цепной линии через 25.

Если положение центроида кривой известно, то площадь соответствующей плоскости вращения можно легко найти по теореме Гульдина. Людмила Фирмаль

• Пять Му =§Х(ы) S = 0、 −8 для Х(е) является нечетной функцией. Из равенства Mu = 0 уравнение (32.28) дает x0 = 0.В дальнейшем、 Пять МХ = ^ гг&. с Как упоминалось выше, 2nMx-Lx. где Lx-площадь поверхности, образованная вращением цепной линии вокруг оси Ox. Поэтому (см.§ 32.4）、 ВХ = па (2В + АВВ; следовательно, МХ =—[2В—а $ б〜^. П. С. Гульдин (1577-1643) швейцарский математик. 33.1.Несобственный Интеграл определение Пятьсот одиннадцать си б б Двигателем 2AZ—; И затем С другой стороны, следует отметить, что длина 28 многожильных линий может быть легко вычислена по формуле (32.15). По Формуле (32.28)、 Р / 0 =(2И-АВВ ^)/ 4бб |.

Смотрите также:

Предмет математический анализ

Площадь поверхности вращения.	Определение несобственных интегралов.
Работа силы.	Формулы интегрального исчисления для несобственных интегралов.