Оглавление:
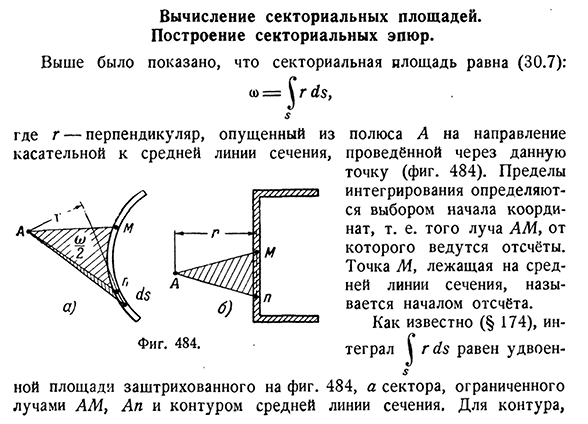






Вычисление секториальных площадей. Построение секториальных эпюр
- Расчет площади сектора. Сектор строительства участка. На рисунке выше показано, что площадь сектора составляет(30.7): Где G-касательная Площадь Нойс, Лидс утра, со=§г ДС, С Перпендикуляром является полюс а(рис. 484). Предел Интеграла определяется выбором начала отсчета, из которого берется образец, то есть пучка АМ. Точка М, которая находится на центральной линии разреза,
называется точкой отсчета. Как мы знаем (§ 174), целое число R c^S удваивается -$ Затенение на рисунке. Сектор окружен контуром 484, а средняя линия участка с АП. Для контура,§ 179] расчет площади сектора 557 Ограниченная прямой линией, площадь деления равна площади контурных линий и временам треугольника, ограниченного между лучами AM и AP (рис. 484, б). Легко заметить, что каждая точка сечения имеет свою собственную область сечения.
Таким образом, область сектора можно рассматривать как Людмила Фирмаль
С Е Т О Р И Л Н У К О Р Д и Н А Т У данной точки. Если вычислить значения секторных областей каждой точки разреза и отложить их в определенном масштабе вдоль средней линии разреза, то можно найти так называемые е н У Р У С Е. В криволинейных контурах сечения длина перпендикуляра g, а следовательно, и величина секторного участка o) изменяется по длине контура в соответствии с контуром[o)=a) (s). В этом случае участок в веерообразной зоне будет изогнут. Если контур сечения представляет собой пунктирную
линию, то для всех точек каждого прямого сечения значение g будет иметь одинаковое значение и график координат сектора (рис. 484, Б) состоит из отдельных прямых участков. Давайте договоримся о знаках. Знак секторных координат для некоторой точки n положителен 485, если подвижный радиус при переходе от выбранного начального радиуса AM к положению AP- ’ вектора вращается по часовой стрелке, а). В обратном случае значение
- со считается отрицательным(рис. 485, б). Если радиус-вектор пересекает контур разреза, то область сектора определяется как алгебраическая сумма двух областей различных кодов(рис. 485, В): К=ГФ-1 — =(Ди-1~(ОД. Как видно из сравнения рисунка(рис. 485, и рис. 485, г), если начало отсчета взято не в точке М, а в другой точке М, то область деления (координаты) одной и той же точки получит разные значения, как по величине, так и по знаку. Нетрудно
заметить, что размер площади сектора также зависит от положения полюса а, где будет происходить строительство.558 основы расчета тонкостенных стержней[гл. XXX До сих пор во всех выводах мы исходили из того, что область сектора состоит из центра изгиба и ее местоположение считается известным. Но иногда построение участка участка сектора осуществляется с использованием каких-либо полюсов, что дает новое значение для координат сектора. Давайте договоримся о выборе поул-позиции и начале отсчета при строительстве участка сектора, следующим образом:
Главным векторным полюсом считается центр изгиба сечения а, Людмила Фирмаль
и в дальнейшем мы построим участок сечения. Отсчет области раздела начинается с определенной точки раздела и называется главной точкой нулевого сектора. Как уже упоминалось(§ 173), подвергают сдержанному скручиванию в»сечении тонких стержней», где точка Ош=0(нулевая точка). Главную^нулевую секторную точку M мы называем нулевой точкой, которая является кратчайшим расстоянием от центра изгиба A. Радиус A-Af называется первичным начальным радиусом, и участок сектора, построенный из него, является участком основной области сектора. В дальнейшем, для того чтобы определить расположение основных секторных полюсов
и главных нулей, необходимо построить секторный участок с произвольным выбором этих точек (рядом с участком балки, чтобы перейти к основной секторной точке, удобно использовать следующую формулу для перехода к новой системе секторных координат). а) изменение опорной точки дуги s эквивалентно изменению интегрального предела функции на=J g ds, С Это приводит к изменению значения площади сектора на постоянное значение. Это видно из перемещения начала отсчета образца из точки M g в точку/, и координаты любой точки получают значение. 486; сектор СО=с о ’ — — — — — — (0м, (30.33) Где < / — секторная Координата точки n при первом запуске образца в точке Mi9 o>M-удвоенная площадь сектора aafjaf,
то есть секторная координата новой начальной точки M, площадь перед образцом§ 179. б) уравнение перехода для переноса полюса из точки LV в точку A можно получить из следующих точек(рис. 487). Возьмем произвольную точку n (y, z) на средней линии сечения (для простоты начало координат y и z берется в точке De). Для точки L e значение базовой области равно=ds * R e. При переносе полюса в точку A (ua, za) площадь базового сектора той же точки n равна: da>A=ds * GA * длина вертикальной га может быть выражена в g0 следующим образом: TA=G9-A^B-BS==G9-Za sin a-y a cos a, где a= — a co sa=as9 ДС= — т -, поэтому: бс1 Или умножьте его на ds,
Смотрите также:

