Оглавление:


Вычисление радиуса кривизны нейтрального слоя для круга и трапеции
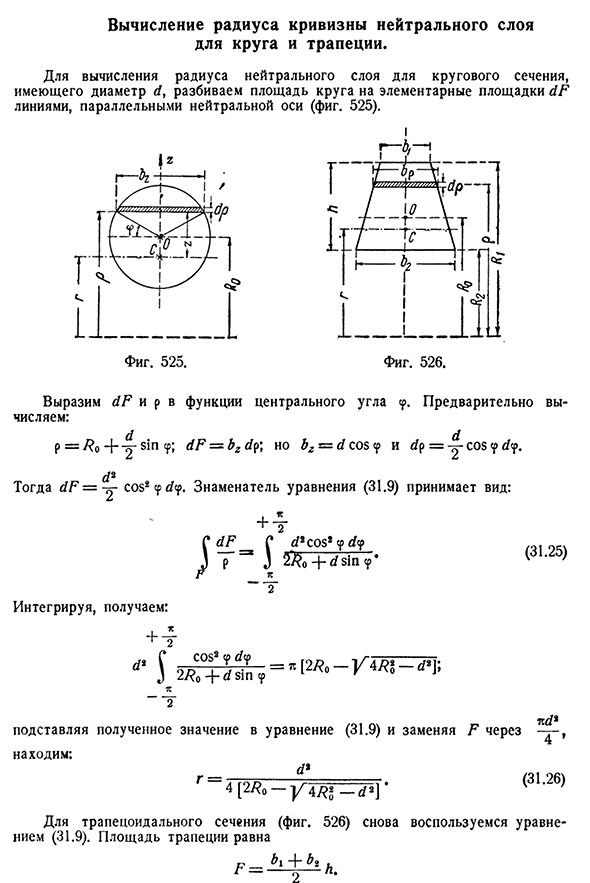
- с площадь окружности на линии dF, параллельные нейтральной оси(рис. 525). Представление и предварительное вычисление
dF и p в функции центрального угла. п=в Sin СР; ДФ=БЗ ДП\а БЗ=Д потому что СР и DP=-^ — соз СР ды. Д2 Затем
dF-cos2dtp. Знаменатель Людмила Фирмаль
уравнения (31.9) принимает вид: Два. С ДФ г D2cos2CP УДС Дж грех СР•(31.25) Интеграция, мы получаем: вс Ted2 присваивает
результирующее значение выражению (31.9)и заменяет F на Поиск: Д2 (31.26) Г4[27?О-d2] • Трапециевидное сечение (рис. Для.) 526) снова
- воспользуемся формулой (31.9). Площадь трапеции выглядит следующим образом F^ _ _ _ _ _ _ _ _ _ _ § 190] приближение. Метод
определения положения является нейтральным. Слой 5 9 3 Ширина трапециевидного сечения на расстоянии р от центра кривизны dF=B (p)rfp. В DF Интеграл I-имеет значение (опущено
промежуточное вычисление): Fn Ф Теперь, по уравнению (31.9), получим: #1+#2 А ~ Людмила Фирмаль
2~ г= (31.27) Если B2=bi, то есть прямоугольник, то это выражение попадает в Формулу (31.16). При # 1=0 получаем выражение, определяющее положение нейтральной оси треугольного сечения:
Смотрите также:

