Оглавление:




Вычисление потенциальной энергии
- Расчет потенциальной энергии. А. При расчете потенциальной энергии мы предполагаем, что не только деформация материала, но и деформация всей конструкции по законам крюка пропорциональна нагрузке. Известно, что при сжатии стержня силой статического натяжения или Р величина работы Ar, а следовательно,
и величина энергии U, равна: U-AR2RD/—2^ -. (21-4)) Для смены (§ 54) Т,/,=AL1Q LA2a&S2G ф ф zo1 все-х П =г г=^р=—(21.5) Время кручения (§ 62) Один. M2l<f2GJp=(21,6) Как и твист, вы можете рассчитать потенциальную энергию чистого изгиба. Конец балки под действием изгибающего момента(фиг. 323) поверните угол 9= -^ -,
где CP-центральный угол / \ Ось балки изогнута дугой радиуса r. Затем Людмила Фирмаль
_M2l_y2EJ2EJ-21(21.7) Фигура. 323. Так как CP=u, — =(13.10) (см.§ 78). Из уравнения (21.4) — (21.7) мы согласны, что потенциальная энергия деформации равна половине произведения силы или пары сил, движущихся в направлении участка, к которому эта сила приложена, и словом «обобщенная сила«мы называем любую нагрузку, которая производит перемещение, соответствующее паре сил, то есть как сил, так и сил.; Смещение, соответствующее этой силе, называется
«обобщенными координатами». «Соответствие» состоит в том, что задача состоит в задаче перемещения участка, в котором приложена рассматриваемая сила, и о вычислении такой потенциальной энергии 103. Перемещение этой работы к этой силе дает нам ценность работы; из-за сосредоточенной силы это линейное движение, расширение в направлении отклонения силы; сила для пары
- одинакова. Тогда можно обобщить формулу (21.4)—(21.7): потенциальная энергия деформации численно равна половине произведения обобщенной силы на соответствующие координаты: I=~, (21.8).) Уравнение(21.4) — (21.7)поскольку эти уравнения не содержат реакций, которые добавляются к элементам и зависят от сил, связанных с ними уравнениями равновесия, из той же формулы видно, что величина искажения потенциальной энергии является функцией второго порядка от»общих координат»системы
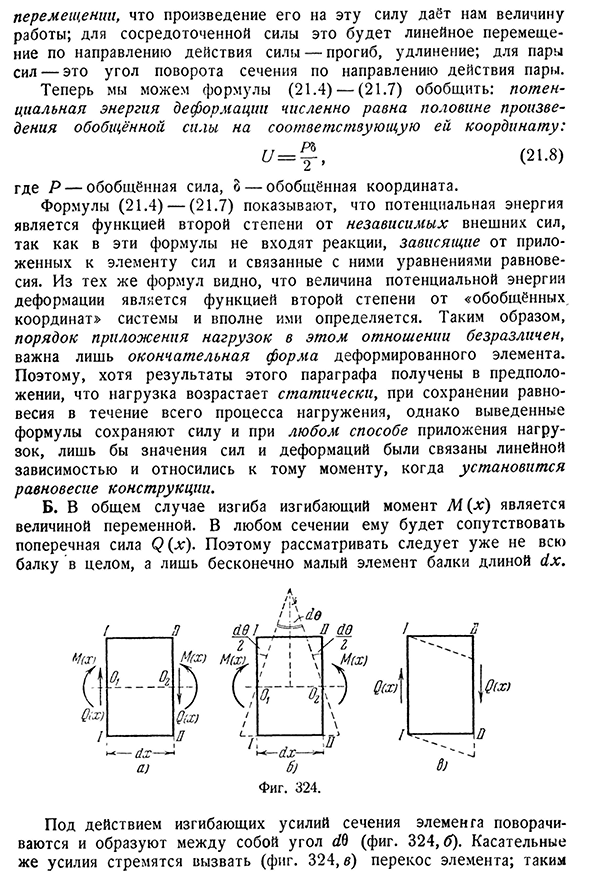
и полностью определяется ими. Поэтому порядок приложения нагрузки в этом отношении безразличен, важна только конечная форма деформирующего элемента. Таким образом, результаты этого пункта получены в предположении, что нагрузка статически увеличивается, сохраняя равновесие на протяжении всего процесса нагружения.、 Б. В общем случае изгибающие, изгибающий момент м(х) — переменная. В любом сечении она будет сопровождаться боковой силой Q (x).
Поэтому необходимо рассматривать не весь пучок в целом, а только микроскопические элементы пучка Людмила Фирмаль
длины dx. Фигура. 324. Под действием изгибающей силы сечение элемента вращается, образуя угловой ДПФ(рис. 324,6). Тангенциальные силы имеют тенденцию возникать(рис. 324, в) косой элемент; takim404 применение понятия потенциальной энергии[гл. XXI Эти смещения от нормального напряжения перпендикулярны направлению касательного напряжения и наоборот. Это позволяет независимо рассчитывать работу изгибающих и тангенциальных сил. Обычно работа тангенциальной силы невелика по сравнению с нормальной работой, поэтому пока мы ее игнорируем. Основные действия обычной силы (как и в случае чистого изгиба) заключаются в следующем: DAP=d U=^ — M (x) dti= =(21,9) Или Фигура. 325. Л г т м2 (* * ) ДХ+2EJ9 Вся потенциальная энергия изгиба получается суммой
длины балки = (21.9) Я Я Для L4 (x), если у вас есть несколько разделов, вам нужно разделить Интеграл(21.9) на сумму интегралов. Рассчитайте потенциальную энергию балки на двух опорах, нагруженных силой Р(рис. 325). Для этого М \ dx2EJ Я.. Л, Р-4″ — н-т М jdx по о==|/ — Х= — — \ — — Х2; Но ПВ& Айсберг»- B. зная величину потенциальной энергии и используя тот факт, что при деформации балки действует только сила Р внешней силы, можно отклонить под действием этой силы следующие зависимости: P2A2^2 А п =-П ф=у, у=^р Дж. Откуда RA * B Зель§ 126] Кастильяно 405 В особых случаях значение отклонения: , / Если я=#= — получаю то, что уже знакомо Р-Р ’48. ’ Иногда, используя небольшое количество внешних активных сил, путем вычисления работы внешних сил можно обойти формулу (21.8
) и произвести определение потенциальной энергии в изгибе. Рассмотрим, например, балку(рис. 326), Пинч-а. и концентрация Р. нагрузки в конце пролетной балки/. На пучок воздействует заданная сила Р и вызванные ею реакции D, MA и NA. Поскольку опорный участок неподвижен, рабочая реакция не возникает, когда балка деформируется, увеличение работы даст только силу P; постепенное усилие. НЛИ Рабочая сила p Ap=U = ±P/=P2 / 3_3f2EJ QEJ-2/3 Если на элементы конструкции действуют какие-то силы, то каждое движение зависит от суммарной нагрузки, поэтому необходимо рассчитать такую генерирующую силу, которая рассчитывается,
действии на балку защемляются концы (рис. 327), приложенная к силе P и свободному концу B vs M, потенциальная энергия имеет следующий вид: L1Oh I1_1, 1.J M I R\Ap-U-2P fB+2M6B-2P^E J2E J+2m\g j2EJj~_R HP M l t~6E J’2EJ2EJJ’ В последних двух примерах, чтобы определить величину внешней силы Ar-U, необходимо было знать величину угла отклонения или поворота в поперечном сечении внешней силы.
Смотрите также:
| Определение деформаций балок переменного сечения | Теорема Кастильяно |
| Постановка вопроса | Примеры приложения теоремы Кастильяно |

