Оглавление:

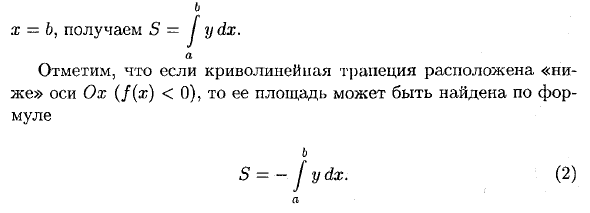
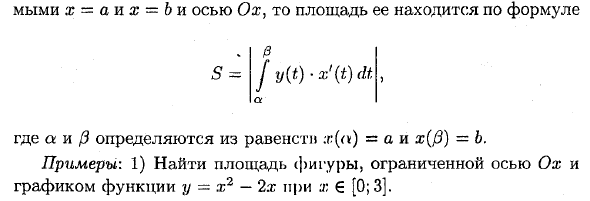



Вычисление площадей плоских фигур
- Расчет площади плана этажа 1. Рассчитать площадь прямоугольного вида сверху координировать Как уже установлено (см. «Геометрическое значение конкретного интеграла»), область изогнутой трапеции, расположенная «над» горизонтальной осью (f (x) ^ 0), представляет собой соответствующий определенный интеграл. Будет равным и = J для дх. дх или с (1)
Уравнение (1) получается путем применения схемы I (метод сумм). Ограничьте кривую трапеции линией y = f (x) ^ 0, x = a, x = 6, y = 0. Чтобы найти область S этой трапеции, сделайте следующее: 1. Любые x € [a; 6] и S = S (x). 2. Дайте аргументу x приращение Ax = dx (функция x 4-Ax 6 S = S (x) принимает приращение AS, которое является площадью «базовой изогнутой трапеции» (обведено на рисунке) вы в).
Используйте схему II, чтобы продемонстрировать уравнение (1). Людмила Фирмаль
Разность площадей dS является основной частью приращения AS с Ax-> 0 и, очевидно, равна площади прямоугольника с основанием dx и высотой y: dS = y • dx. 3. Интегрируйте полученное уравнение между x-a и х х дх б Получить x = b, S = J ydx. Если изогнутая трапеция находится «ниже» оси Ox (f (x) <0), ее площадь можно рассчитать по следующей формуле. б S = -j y dx. но
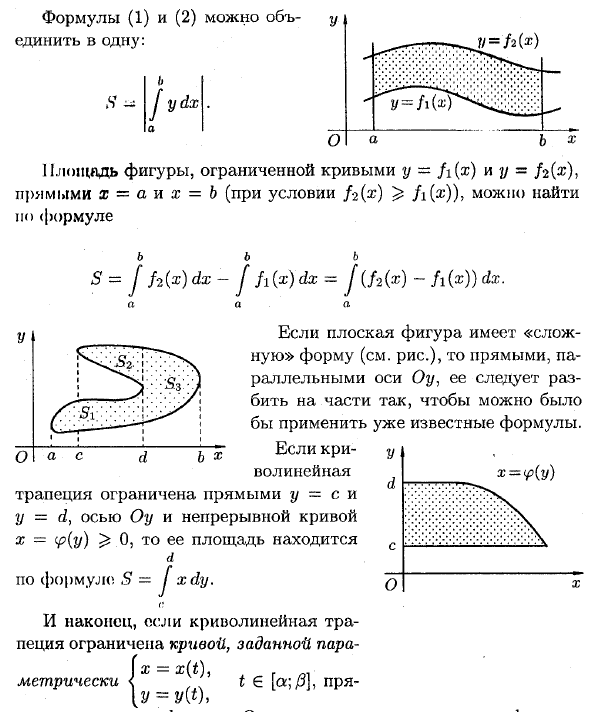
Выражения (1) и (2) могут быть объединены в одно. и J y dx R / = / 2 (я) S ~ Найти площадь фигуры, заключенную в кривые y — \ {x) и y = / 2 (2), прямые x = a и x = b (условие fz (x) ^ / i (®)) в формуле вы можете в и S = I / 2 (x) dx-Ih (x) dx = J (f2 (x) -f1 (x)) dx. в я ^ J.S2 g. 1 й «•. ■■ SsX о d Б я и Если плоская фигура представляет собой «сложную» форму (см. Рисунок), ее следует разбить на части, чтобы можно было использовать прямую линию, параллельную оси Oy, для применения известной формулы. если х = <р (у) о X Тем не менее, формула S = J xdy.
| Несобственные интегралы | Вычисление длины дуги плоской кривой |
| Схемы применения определенного интеграла к нахождению геометрических и физических величин | Действительные числа. координаты точки на прямой |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- И, наконец, изогнутая трапеция представляет собой пару- [x-x (t) <‘T 6 [ct; / 3] непосредственно в метрике 13 / = 2 / (0 » Трапеция ограничена прямыми линиями y = c и y = d, осью Oy и непрерывной кривой x => 0, а ее площадь равна Для x = a и x = b и оси Oy площадь определяется как 5 = дт фу (т) .х ‘(т) но Где a и a определяются из уравнения: r (a) = a и x (0) = b. Пример: 1) Найти область фигуры, окруженную x G [0; 3] осью Og, и график функции y = .m2-2.m.
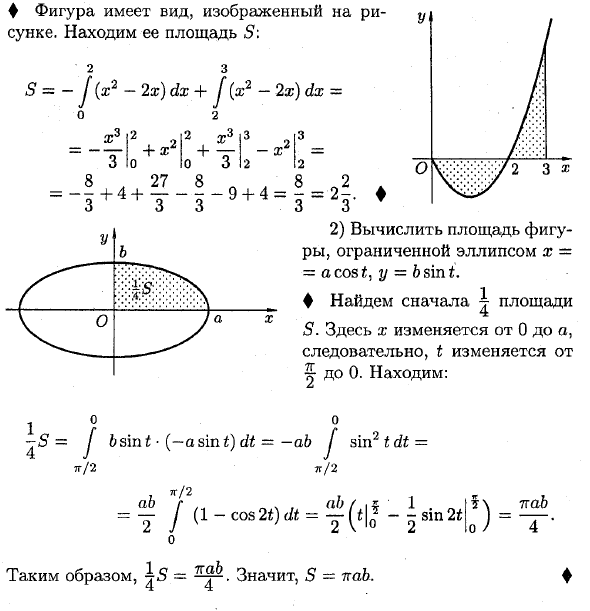
♦ Рисунок такой, как показано на рисунке. Найдите область 5. 2 секунды S = -J (x2-2a?) Dx 4-J (x2-2®) dx = 3,2 хорошо X да Sii ^ о 3,3 3 ‘O 10 3 12 8 27 8 с, 8 „2. = —4-44- —— 9 + 4 = — = 2-. ♦ 3 3 2) Рассчитайте площадь фигуры, заключенную в эллипс x = a cos y = 6 sin t. ♦ Сначала найдите область 5. ^ о -5 = J bs’mt • (-asint) dt = -ab J sin2 tdt = TT / 2 I / 2 тф / 2 ab r L., rtft / .ifi «1. L | t \ ttb Так = следовательно 5 = 7bb.
Здесь a: изменяется от 0 до a, поэтому t изменяется от ^ до 0. Людмила Фирмаль
Расчет площади плана вида координировать «Найти плоскую форму (г и ( р — полярная координата). Для решения этой проблемы используется схема II-разностного метода. Рассмотрим часть требуемой площади S как функцию угла 0 (если ip = 0, 5 (n) = 0, если 0 и радиусу r угла наклона центрального угла. Следовательно, dS = ^ r2 • d <p ; .’J) Интегрировать полученное уравнение в диапазон <p-a 0 ip = /? Получите нужную область S = i J r’2 (<p) dip.
Пример: «3 лепестка розы» g-a cos \ <p Найдите область, указанную на рисунке. ♦ Сначала найдите половину площади одного лепестка розы, всю г часть. Площадь диаграммы: 1 1 1 11/6 1 qS = 2 / (ac ° s3ip) 2dip = -a2 J- (l + cos6ip) d (p = Или. 7 г / б. 1. l | tg / bv a, 7g lch pa ‘ 24 ‘ То есть = 5 = ♦ Если плоская фигура имеет «сложную» форму, луч заканчивается От полюса его следует разделить на изогнутые сектора, Найти площадь, применяя полученную формулу Gz. Следовательно, диаграмма, показанная на рисунке: но 1 1 1 s = 2 / ri ^ -rj ri d <P 2 / T’g d (p р

