Вычисление площадей

Вычисление площадей

Вычисление площадей. На данный момент формула для вычисления площади некоторых плоских областей является derived. At в то же время он использует простейшие свойства плоской формы (полигон, сектор), известные из базовой математики. Например, если объединить эти фигуры, которые не имеют общей внутренней точки, добавляется область. Однако это утверждение строго доказано в§ 44.1. Теорема 1.Определите функцию, неотрицательную, непрерывную на интервале[a, b].Площадь составляет 8 комплектов 0 = {(х, г).A x b, 0 y [(x)} представляется следующей формулой Множество O-это открытая граница set. In фактически, его ограниченность основана на том, что функция/, смежная с интервалом[a, b], ограничена.

Области без границ, где границы являются подобными контурами, называются внешними (для данного контура). Людмила Фирмаль

• Указывает, что набор O открыт. (g-0, V°)> 0;тогда отсчет O y0 /(*)) •r| 0 и т. д. V0-Ts V0 V0 + Ts1 (x0)-из-за непрерывности функции/ x0, x0, x0 +δ) окрестность неравенства (x) для всех x∈(x0-δ, x0 + δ) P (((x0-Y0)\ b, m) принадлежит множеству O, что означает, что (x0-x0, x0-y0) явно его внутренняя точка. Границы множества O содержатся в графе функции/, сегментах [a, b] оси Ox и соединениях сегментов[0, f (a)] и[0, f (b)] прямых x = a и x = B. It обычно называется кривой трапецией (см. Рисунок 90), которая генерируется графом функции/. Доказательство. пусть m = {x, -}; = o-разбиение отрезка [a, b].Показывает замкнутые полигоны, состоящие из всех прямоугольников формы в Ox и в§x Если вы представляете набор внутренних точек в CX и qx как Cx и.

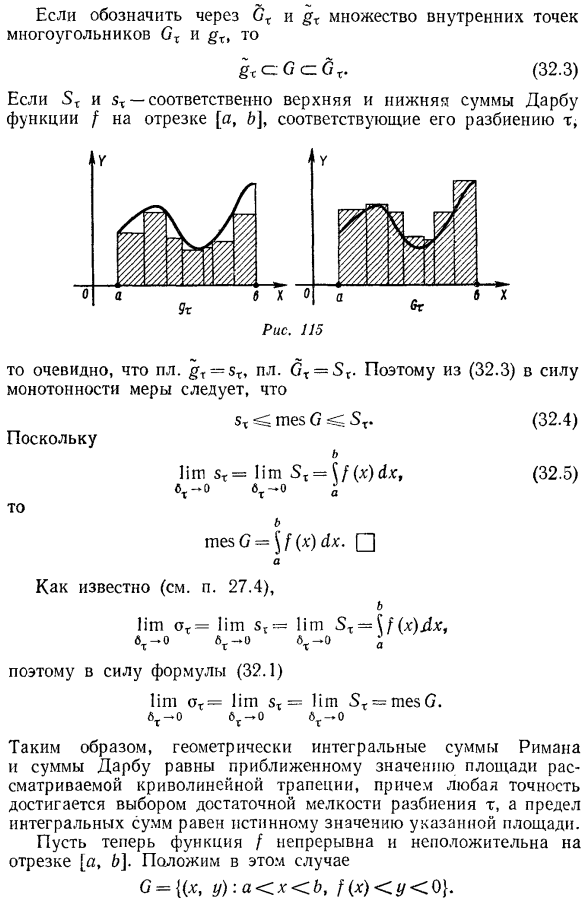
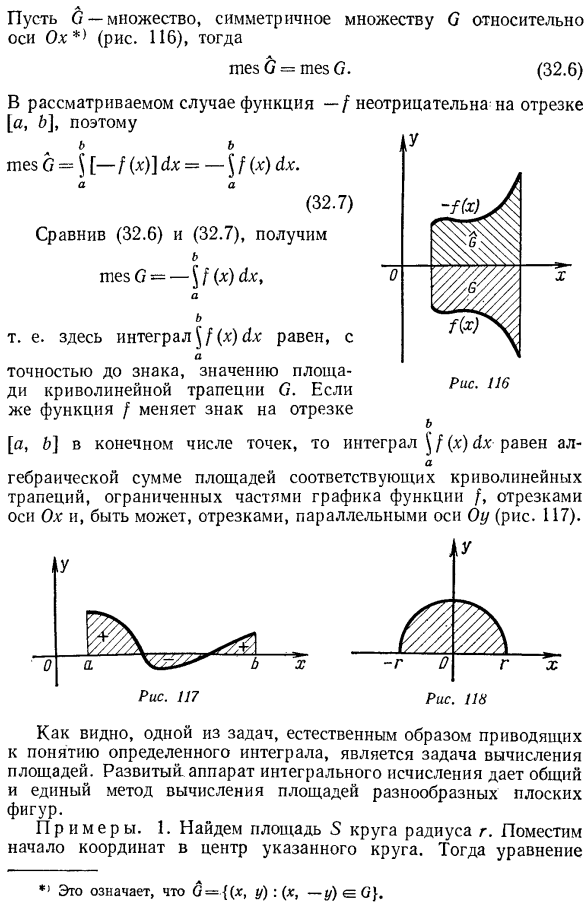
Если 8X и 5T-верхняя и нижняя суммы дарбоэу функций сегмента [a, b], соответствующих разбиению m, соответственно、 Поэтому геометрически интегрированная сумма Римана и Дарбоха равна приближенной площади рассматриваемой трапеции кривизны, точность достигается выбором достаточной тонкости разбиения m, а предел интегральной суммы равен истинному значению указанной площади. Здесь функция [интервал [a, b], чтобы сделать его непрерывной и неположительной функцией. Положите его в этом случае Пусть C-множество, симметричное множеству O относительно оси Ox *(рис. 116). В рассматриваемом случае функция/ не отрицательна в отрезке[a, b], поэтому.

• Точность знака, значение площади кривой трапеции С. Если функция / изменяет знак отрезка [a, b]в терминах конечного числа Интеграл§ / (x) dx равен Алгебраическая сумма площади функции / графа, отрезка оси Ox и, возможно, соответствующей кривой трапеции, разделенной отрезком, параллельным оси Oy (рис.117). Как видим, 1 из задач, которые естественным образом приводят к понятию конкретного интеграла, является задача вычисления площади. Разработанный аппарат интегрального расчета обеспечивает общий и единообразный метод расчета площади различных плоских фигур. Образцы. 1.Найдите область из 5 окружностей радиуса r. поместите начало координат в центр указанной окружности.

Тогда уравнение Форма полукруга в верхней полуплоскости равна y = y72-x2(рис. 118). таким образом, согласно теореме 1, Формула (32.1) вычисляет площадь полукруга радиуса r. (При вычислении интеграла переменная x = rco $ {была заменена), искомая площадь окружности будет равна π2. Аналогично, существует также секторная область (радиус r) окружности, соответствующая центральному углу p. для простоты предположим^ ^ф^^ ^ / 2 (рис. 119). 2.Найдите область 1, ограниченную 1 дугой оси Ox и синусом (рис. 120). Здесь, как всегда, когда мы говорим о области, ограниченной некоторой кривой с простым замкнутым контуром (см.§ 16.1), мы всегда имеем в виду граничную область, где границей является этот контур.

В рассматриваемом случае внешняя область является «внешней стороной» заштрихованной области на рисунке. Людмила Фирмаль

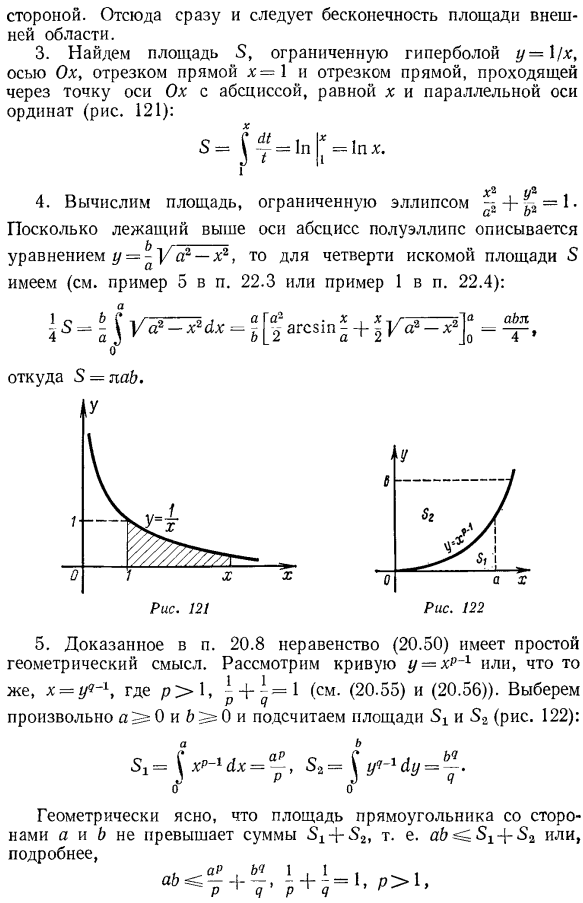
• 120.Во внешнем всегда есть бесконечная область area. In фактически, каждая кривая имеет границу (см.§ 16.3). так, внешняя область простого контура, например, квадрат любого размера Сторона. Отсюда сразу же следует бесконечность внешней области. 3.Найдите область, ограниченную линией (рис.121) через гиперболу y = 1 / dg, ось Ox, линию x = 1 и точку, где абсцисса равна x и параллельна оси ординат. 4.Вычислите площадь, ограниченную эллипсом+ p == 1. Полуэллипсы над абсциссой описываются формулой y = ^ y ^ a2-x2, то есть за 4 минуты 5 требуемой площади (см. Пример 5 на 22.3 или Пример 1 на 22.4). 5. Неравенство, доказанное в разделе 20.8 (20.50), имеет простой геометрический смысл. Кривая у = Х? X или что-то, о чем стоит подумать х = уб-х, где、1、^ + ^ = 1（（20.55）и (20.56)).Произвольно выберите ^ 0 и B ^ 0 для вычисления площадей и 52(рис. 122). Площадь прямоугольника, края которого не являются&, геометрически ясна.

Смотрите также:

Предмет математический анализ

Определение меры (площади) открытых множеств.	Объем тел вращения.
Свойства меры открытых множеств.	Вычисление длины кривой.