Вычисление определенного интеграла при помощи первообразной функции

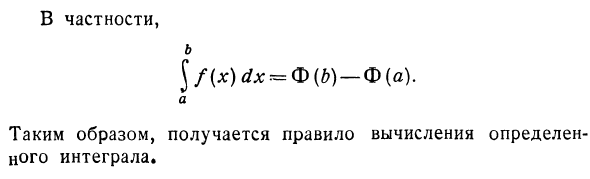
Вычисление определенного интеграла при помощи первообразной функции

• Вычислить определенные интегралы, используя примитивные функции Рассмотрим изогнутую трапецию, окруженную осью Ox и кривой y = f (x) y с прямыми линиями aA и xB, параллельными оси Oy (рис. 82). Если вы измените г, то есть переместитесь вправо на xB определенной трапеции, площадь изменится. Таким образом, рассматриваемая область зависит от положения стороны xB, которая определяется числовым значением x. Таким образом, область является функцией х. Указанная область обозначается как F (x), а затем как pl. aABx = F (x).

. И из главы 4. IX знает, что производная площади изогнутой трапеции равна f (x) dx. так L dF (x) = d \ f (x) dx = f (x) dx в G (х) Следовательно, площадь изогнутой трапеции Обратная производная функции / (x), ограничивающая эту трапецию.

Поскольку § 2 показал, что площадь представлена определенным интегралом, J f (x) dx = F (x) Людмила Фирмаль

Обратная производная функции f (x) обозначается через Φ (x). тогда L F (x) = <b (x) + C {). о Верхний предел рисунка составляет 82. Интеграл, равный (рисунок 82), Другими словами, когда правая и левая стороны объединены, площадь равна нулю. Это означает, что F (a) = Φ (a) + C = 0. Отсюда видно, что C = -Φ (a). Подстановка полученного значения C в уравнение () дает: или / 7 (x) = Φ (:):) — Φ (a), L J / (*) dx = d) (x) -Φ (c). 27 SG особенно $ / (*) Dxr. но Таким образом, вы получите новый интеграл.

• = Φ (b) -Φ (a). Правила расчета определены Для вычисления конкретного интеграла J / (*) вам необходимо: но 1) Найти одно из анти производных Φ (x) подынтегрального выражения f (x). 2) Рассчитать значение функции Φ (x) как x = b, т.е. Φ (?); 3) Рассчитать значение функции Φ (π;) для x ay, т.е. Φ (a); 4) Вычтите второй результат из первого результата: Φ (b) -Φ (a) б

Пример 1. Рассчитать интеграл J xx dx. с того времени но B sz = x2> тогда A x * dx = ~ -. Результаты матча но Предложено в § 1 этой главы. L 2 Пример 2. ^ sin l: flfx. (-Cos l 🙂 ‘= грех ху о f (l;) = -cos l:. В результате Φ (-y) = -cos (~ f «) л_2 φ (0) = -cosO = -1, поэтому 5 Sinxdx = 0 — (- 1) = 1. о

При вычислении конкретного интеграла используется знак перестановки [то есть, если Φ (π) является обратной производной функции / (*), б J / (x) dx = [Φ (x)] ba = Φ (b) −Φ (a). Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Приближенное вычисление площадей криволинейных трапеций	Свойства определенного интеграла
Определенный интеграл	Задачи на применение определенного интеграла