Оглавление:

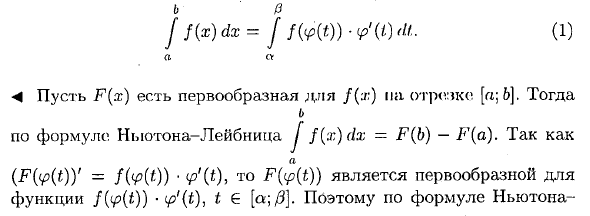

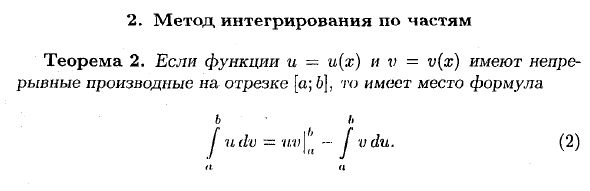

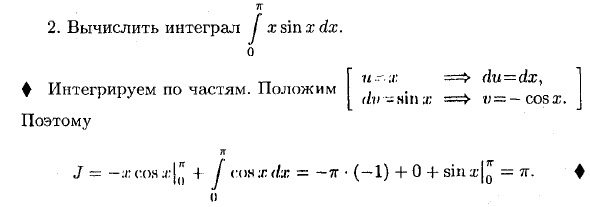
Вычисление определенного интеграла
- Расчет конкретного интеграла Простой и удобный способ вычислить конкретное целое число Непрерывная функция J f (x) dx является уравнением Нейтона-Лейбница: J f (x) dx = F (®) | * = F (b) -F (a). L Этот метод применяется во всех случаях, когда обратная производная функции F (x) найдена для подынтегральной функции f (x). Например, ^ s’mxdx = -cosx | ^ = ~ (cos7r-cosO) = 2.о
1. Интеграция методом замены (замена Variable) б Предположим, вы создали перестановку x = ip (t) для вычисления интеграла J f (x) dx непрерывной функции. «Теорема 1. Если: 1) Функция x = (Р) = b, тогда но J f (x) dx = J f {* p (t)) • ip ‘(t) fU. (1) Сс <4 Пусть F (x) — обратная производная от f (x) над (Uggreg (a; 6). б Согласно уравнению Нейтона-Лейбница J f (x) dx = F (b) -F (a). с того времени (F (ip (t)) ‘= f (v (t)) • <p’ (t) и F (ip (t)) являются примитивами функции f (ip (t)) — tp’it). t £ [a; 0].
Методы подстановки переменных и методы интеграции компонентов широко используются для вычисления конкретных интегралов. Людмила Фирмаль
Следовательно, согласно уравнению Ньютона:Лейбниц 0 / / io) • ✓ (<) = = = fr) -г) = Per * В = F (b) -F (a) = J f (x) dx. ► » Уравнение (1) называется уравнением, которое заменяет переменную определенным интегралом. Пожалуйста, обратите внимание на следующее: 1) При вычислении конкретного интеграла методом подстановки нет необходимости возвращаться к старой переменной. 2) Во многих случаях вместо замены x = ip (t) используется замена t = g [x) \ 3) Не забудьте изменить пределы интеграции при смене переменных! 2 Пример: J x2y / 4-x’g dx рассчитывается. о ♦ Введите x = 2sin /, а затем dx = 2costdt. если x = 0, t = 0, если x = 2, следовательно, t = 2 __l / 2 J X2 \ / 4-x r = J 4 sin2 £ \ / 4-4 sin2 t x2 • 2 cos t dt- Ах ах я / 2 я / 2 „тг / 2 = 16 sin’2 * cos’2M * = 16 | ^ sin2 2tdt-4 J-cos4t) dt-
Метод интеграции по иску Теорема 2. Функции u = u (x) и v = v (x) находятся в интервале [a; 6], и выполняется уравнение б-б l ‘и dv-uv | -J vdu. (2) Функция uv является обратной производной непрерывной функции u’v + hell /, поскольку существует уравнение для сегмента M a; B ‘= u’v + uv’.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Тогда согласно формуле Ньютона Лейбница: и J (уф + уф ‘) дх = уф \ так и J v- и ‘dx + J uv’ dx = uv \ bn О, о, о J vdu + J и dv = uv • => J udv = uv \ ‘n-J vdu. Уравнение (2) называется интегрированием подвыражением конкретной интеграции. Пример: 1. Рассчитать J x In i dx. и = 1 и x du = -dx, х -f Используя уравнение (2) ♦ Предположим, что вы получаете DV = XDX [x In x dx = ~ • In- [~ r • -dx = Y 2 11 Y 2 a; e2 „la: 2 * e2 e2 1 1 1, / •>Рассчитать интеграл J xs’mxdx. о ♦ Интеграция деталей.
Положить в N J = -a: соя + у soxxdx — 7G 71-х ду = дх> dv-n в x — = — cos x. (-1) + 0 + sinx’l * = тг. Людмила Фирмаль

