Оглавление:






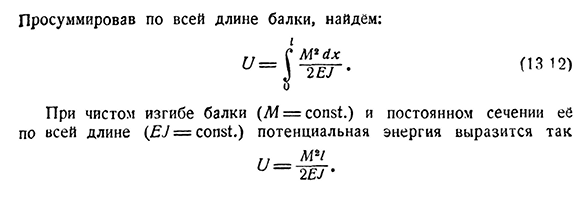

Вычисление нормальных напряжений при изгибе. Закон Гука и потенциальная энергия при изгибе
- Расчет нормального напряжения изгиба. Закон крюка и потенциальная энергия изгиба. A. возьмите балку, которая получает чистый изгиб по паре 711(рис. 182). Используя метод поперечного сечения, балку сечения 1-1 разрезают на 2 части с учетом равновесного состояния клипсового сечения, например, слева, показанного на рисунке. 182 внизу. Из-за простоты прорисовки балка берется прямоугольного сечения. Отрезная часть не деформируется, так как фактически кривизна балки ничтожна по сравнению с ее размерами. Линия пересечения плоскости симметрии поперечного сечения и балки принимается за ось z (положительное направление снимается вниз), нейтральная ось поперечного сечения
является осью y, а высота балки до сих пор неизвестна. Ось X берется вдоль нейтрального слоя, перпендикулярного оси y и оси Z. Если вы выберете вокруг любой точки с координатами y и Z базовую область dF, сила, действующая на нее, указывает, что это dN=dF. Отрезанная часть балки находится в равновесии под действием внешних сил, образующих пару 714 и вертикальной силы рфтв, которая заменяет отброшенную часть балки. Для равновесия эта система сил должна удовлетворять шести уравнениям статики. Сначала запишем уравнение проекции на 3 оси x, y, Z.
Так как проекция пары 714 на любую ось равна нулю, то эти уравнения Людмила Фирмаль
делают сумму проекций вертикальной силы dN на ось равной нулю. Заменив сумму этих сил по всему поперечному сечению интеграцией, получим.: Около < ФСР = б.(13.1)л 2K=0 и v z=o преобразуется в идентификатор вида 0=0, поскольку сила d N=a D F проецируется на точки На этих осях. Построим уравнение моментов для осей X, y и g. Отметим, что пара м находится в плоскости хо Z и, следовательно, не дают момента на оси Ох и Oz.262 расчет нормального напряжения изгиба[гл. ПВТ Сила ду=АДФ параллельна оси X, таким образом,=o изменения в код: =W-VdN>z=Q или M — ^A d F » z=0, Откуда Дж А З Д Ф=М(13.2) VM,=0;^d N^y=Q или^d F * y=0. (13.3) Поэтому из шести уравнений равновесия можно использовать только
.- — o или=0 или£М Г=0 или (13.1′)) (13.2 е (13.3′)) Однако полученных трех статических уравнений недостаточно для определения величины нормального напряжения, так как с изменяется Первоначальная длина По неизвестному пока закону зависит расстояние z-dF до нейтральной оси. Поскольку положение нейтральной оси Y неизвестно, это расстояние (фунт) также неизвестно. Рассмотрим вариант балки, для двух почти бесконечных участков 1-1 и 2-2 выберем из нее элементы длины dx. Представление этого элемента до и после преобразования показано
- на диаграмме. 183. Для уточнения рисунка варианты элементов показаны сильно преувеличенными. Оба поперечных сечения, оставаясь плоскими, вращаются вокруг нейтральной оси (фасады точек Oh и O2), образуя угловую da. Нейтральный слой обозначен пунктирной линией. Линия OiO2, принадлежащая нейтральному слою, сохраняет dx после деформации. Все волокна над нейтральным слоем будут короче и длиннее.§ 78] расчет нормального напряжения изгиба 263 Найти относительное удлинение любого волокна AB, расположенного на расстоянии z от нейтрального слоя и растянутого напряжением A. Первая длина этого волокна D x=o1o2=p rfa. После деформации длина дуги AB равна^A B=(p—z) da.. Абсолютное
удлинение рассматриваемых волокон A/=(p-1-z) d z—p dz=z dz. Удлиненность is_ _ Z да Z от Р Д~т р’ То есть удлинение волокон пропорционально расстоянию до нейтрального слоя. Здесь p-радиус кривизны нейтрального слоя, а значение выбранного (длина бесконечно малого) элемента можно считать постоянным. Предположим, что при изгибе волокна не давят друг на друга, а каждое волокно испытывает простое (линейное) растяжение или сжатие.: а=ЕГ и Е-З а= — — — -. П (13.4) м АКС(м) Фигура. 184. Ось. Поэтому максимум на верхней и нижней кромках сечения- Уравнение (13.4) показывает, что величина вертикального напряжения изгиба изменяется прямо пропорционально расстоянию z рассматриваемой точки подвешивания от нейтрального слоя.
Следовательно, давление распределяется по высоте поперечного сечения по линейному Людмила Фирмаль
закону. / I z=0 и нейтральной оси при a=0;при перемещении в зону сжатия (выше оси\neutral) a с z меняет знак на минус (сжатие), и характер распределения напряжений нейтрального значения, достигающего z=zmax, показан на рисунке. 184. Уравнение (13.4) дает только характер распределения нормальных напряжений в поперечном сечении, но так как расположение нейтрального слоя на высоте поперечного сечения неизвестно, то ни p, ни z неизвестны.、 B. To определив а в зависимости от изгибающего момента, обратимся к комбинированным решениям уравнений (13.4) и статических уравнений (13.1), (13.2) и (13.3), полученным из рассмотрения деформации.264 расчет нормального напряжения изгиба[g l. XIII Подставляя значение o из выражения (13.4)в
выражение(13.1), получаем: в X=0 или^—З Д ф^В. От — = const. 0, тогда ВСЗ = В.(13.5)) Этот Интеграл представляет собой статический момент поперечного сечения относительно нейтральной оси. Итак, поскольку он равен нулю, нейтральная ось проходит через центроид сечения. Так как центр тяжести находится на оси симметричной Og, то пересечение этих двух осей O является центром тяжести сечения, а ось ox-осью стержня. Таким образом, положение нейтральной оси и нейтрального слоя хорошо определено. Нейтральный слой включает в себя центр тяжести всех секций стержня. Затем подставим то же уравнение(13.4) в уравнение (13.3): — 0 или y^z y d F-0. Это следует Джей З м д ф=0. (13.6) Полученный Интеграл-сумма
произведений базового участка на расстояние до осей координат-называется центробежным моментом инерции для оси y и оси Z. Центробежный момент инерции положителен и может быть отрицательным, поэтому, поскольку координаты базовой площадки могут иметь разные знаки, они могут обратиться в нуль. По условию (13.6), в нашем случае центробежный момент инерции, который обычно обозначается знаком Джей З г=§з Г Д Ф, Г Вам нужно перейти к нулю. Для каждого участка dF с координатами g, y слева от оси z найдите один и тот же симметрично расположенный участок справа от оси z, поскольку поперечное сечение симметрично относительно оси Og, координата z этих участков будет одинаковой по величине и знаку, а координата y будет одинаковой,§ 265
Абсолютное значение то же самое, но знак противоположный. И так оно и есть.、 зы ДФ Ф Уравнения; подстановка Она делится на две суммы, равные размеру знака и противоположные. Таким образом, этот Интеграл симметричного сечения всегда равен нулю, и уравнение(13.6) будет идентичным. Наконец, используя последнее выражение в нем(13.4)、: 2^=0,\—z4f=m ? п Покажите СП — ^З^Д Ф. (13.7) Или-z * dF-M. Этот Интеграл, то есть сумма произведений фундаментальной области на квадрат расстояния от оси, называется моментом инерции области относительно оси y или осью y, обозначаемой Jy. Поскольку ось Y является нейтральной осью, то есть моментом инерции площади поперечного сечения балки относительно нейтральной оси 1). Тогда только что преобразованное из уравнения (13.2) получим: Или (13.8) Подставляя найденное значение в выражение(13.4), можно увидеть следующее: Таким
образом, нормальное напряжение в любой точке сечения прямо пропорционально изгибающему моменту и расстоянию от нейтральной оси точки, А напряжение сечения относительно нейтральной оси. Нейтральная ось проходит через центр тяжести сечения и перпендикулярна рабочей плоскости силы. Момент инерции сечения, Как видно из Формулы (13.7), измеряется в единицах длины четвертой силы и зависит от формы x) в дальнейшем расчет нормального изгибного напряжения для нейтральной оси y 266[глава XIII]. И размер секции. Практические методы его расчета для различных участков приведены ниже. Чтобы установить физический смысл этого значения, измените выражение (13.8): 7=<13л°) Таким образом, чем больше Момент инерции сечения J в заданный изгибающий момент, тем больше радиус кривизны нейтрального слоя, а следовательно, и ось балки меньше. Величина момента инерции характеризует способность балки сопротивляться искривлению в зависимости от размера и формы поперечного
сечения балки. Модуль упругости е характеризует ту же способность балки сопротивляться искривлению, но зависит от материала балки. Произведение EJ называется изгибной жесткостью балки, и чем она больше, тем меньше она изгибается под действием заданного изгибающего момента. Кривизна оси балки связана с взаимным вращением сечения и г.; длина отрезка 0 (7=dx, как видно из чертежа (фиг. 183) равен КПК. Таким образом, угол поворота двух соседних секций Вместо этого подставьте значение М ЭДЖ Возьми: Окружной прокурор= M dx EJ (13.11) 1^ П То есть деформация в изгибном повороте участка da, а также кривизна оси балки прямо
пропорциональны величине изгибающего момента и обратно пропорциональны жесткости балки. Многократно оцененная потенциальная энергия накопленного пучка легко вычисляется в§ 62. При изгибе бесконечно малого отрезка балки длиной d x t работа изгибающего момента углового перемещения da будет равна: да-да-АФ.
Смотрите также:

