Оглавление:
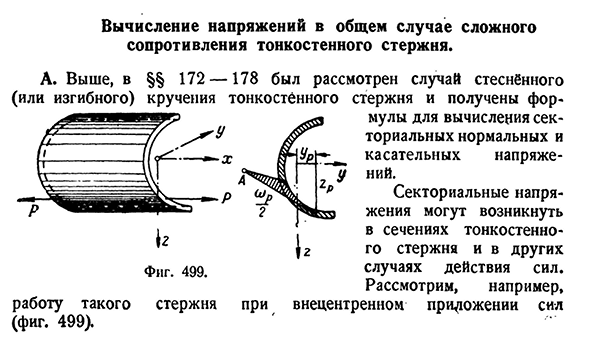




Вычисление напряжений в общем случае сложного сопротивления тонкостенного стержня
- Расчет напряжений в общем случае комплексного сопротивления тонкостенных стержней. A. In выше, ⧧ 172-178, рассмотрим случай ограничения (или изгиба) скручивания тонкостенных стержней.、- Фигура. Четыреста девяносто девять Такая работа(рис. 499). Из стержня Мул для вычисления нормального напряжения сектора
и тангенциального напряжения. Напряжение сектора может возникнуть в случае действия секций тонкостенных стержней и других сил. Например, для внецентрового приложения силы§ 1 8 2] Расчет напряжения при комплексном сопротивлении 5 7 1
Условия равновесия выражаются формулой(30.1), (30.2), (30.3) и (30.17) Людмила Фирмаль
принимает форму этого случая (по сравнению с рис. Четыреста шестьдесят девять): < 5dF = Р\ Ф AdFy=Пип, ф Я (30.52) где B^~bimoment, B$=P (yr. Таким образом, если продольная сила приложена в точке поперечного сечения, где координата сектора<o равна нулю, то бимомент изгиба кручения B также равен нулю. Только в этом
частном случае внецентрового приложения напряжения P (Yu p=0) гипотеза плоского сечения справедлива: сила не сопровождается скручиванием, растяжением стержня и в остальных случаях (в ■ yr = £0) растяжением дополнительного центра тонкостенного стержня открытого профиля, Поэтому, например, в случае зетового профиля, расчет тонкого стержня 572 основания[гл. XXX Как упоминалось выше
- (§ 180), участок секторной площади имеет вид, показанный на рисунке. 498 следовательно, вторая Координата точки о, лежащей в центроиде сечения, представляет собой 500-пунктирную линию, проходящую через центроид сечения, или если центр тяжести сечения приложен к центроиду Z. Нормальное напряжение в поперечном сечении стержня Z-профиля определяется по следующей формуле: I P \ V® Сечение такого стержня после
деформации не является плоским, даже если фиксация его концов не препятствует свободному износу концов. B. Изгибное кручение также возникает, когда поперечное изгибающее стержень усилие лежит на основной поверхности инерции, не проходя через центр изгиба. При плоском поперечном изгибе нормальное напряжение определяется по формуле:. В (L * U один) Для более общего изгиба(косой изгиб, или в основном направлении): (30.53)
Второй поворот. (30.54) Величина димера изгиба-кручения в этих случаях зависит от эксцентриситета внешней силы относительно линии центра изгиба, интегрируя дифференциальные уравнения (30.27) Людмила Фирмаль
и (30.29), или согласно таблице 27 (177). Наконец, в случае совместного действия продольных и поперечных сил с изгибным кручением формула нормального напряжения будет иметь следующий вид: o=++(30.53) Один. Дж, дж, дж, дж. с. Здесь бимомент B изгиба-кручения является возможностью поперечных и продольных сил. Тангенциальное напряжение в этих случаях возникает под действием поперечных сил и вследствие скручивания стержня.§ 183] пример расчета напряжений 573 Величину тангенциального напряжения от сил Q и o можно определить по формуле: _. М^Г А Д’jy*» (30.56) Первые два члена формулы определяют тангенциальное напряжение от составляющей поперечной силы Q-сектора тангенциального напряжения, обусловленного действием изгибающего момента.
Следует отметить, что оба касательных напряжения действуют вдоль контура сечения. Величина 8 во всех отношениях уравнения обычно измеряется толщиной стенки по контуру, с? — Статические моменты отсеченных участков относительно главной оси инерции; Jy и Jz-момент инерции всего участка относительно одной и той же оси; части участка; — главный веерообразный момент инерции участка. Кроме того, тангенциальное напряжение, рассчитанное по формуле (30.56), прикладывается с тангенциальным напряжением от чистого кручения, достигающим наибольшего значения в середине кромки стенки, и вычисляется по формуле (11.37) [§§ 67,173 и [ … ]
Смотрите также:

