Оглавление:






Вычисление напряжений при колебаниях
- Расчет напряжений при вибрации. Упругая система, выведенная каким-то образом из равновесия, становится колебательным движением. Колебания возникают вблизи положения упругого равновесия, при котором нагруженная система имеет статическую деформацию, и соответствующее статическое напряжение pz (в зависимости от вида ос или TC-деформации). При вибрации
к статической деформации добавляется динамическая деформация, зависящая от вида вибрационного движения и величины диапазона колебаний (амплитуды) ОГ. В связи с этим изменяется и напряжение PZ. Поэтому при расчете колебательной системы на прочность необходимо уметь рассчитывать динамические
добавки для статических деформаций и соответствующих им напряжений. Часто Людмила Фирмаль
характер колебаний системы можно определить по одному значению (одной координате). Одна степень свободы системы называется системой; ) Л О Ж К и Н С К и й Л О Г И Л И Л У Р Е А. и., курс теоретической механики, 1940, часть первая, §§ 91, 92, 150— 154; Н И К О Л А я Е. Л., Теоретическая механика, 1939, Часть II, §§ 32, 33, 35, 36, 37; 6y8 учет инерционных и колебательных сил[гл. XXXV Таковы, например, растяжимые или сжатые пружины незначительного веса
с нагрузками на концах, приводящими к продольным колебаниям. 590, например, колебание в направлении, перпендикулярном его оси. В случае вибрации системы определенной степени свободы, полной деформации системы в любом разделе, чтобы проверить прочность системы на добавление статической деформации с дополнительной деформацией во время вибрации, очевидно, нужно найти наиболее опасную часть в процессе вибрации общей величины деформации».
- В простейшем случае к этому следует добавить максимальную статическую деформацию ос1пах с максимальной амплитудой колебаний D, т. е. — БС Макс-Д-Ж-А-ОС тах м_ _ из б R: — макс 20°C / (35.19) Пока система деформируется в пределах упругости, напряжение пропорционально деформации. Поэтому RL=RS(1+1=KJC, (35.20) \С лучшими / Куда? (35.21) С Шахом — Коэффициент динамичности в колебаниях. Условие прочности в этом случае выглядит следующим образом: RL=KLR с^[R]-(35.22) так, чтобы он не менял своего направления из-за силы инерции, он находит динамическое напряжение и проверяет силу изменения Как
известно, дифференциальное уравнение движения колебательной нагрузки Q в случае свободных колебаний выражается уравнением равновесия, которое представляет собой расчет напряжения при колебаниях 689, помимо внешней силы (масса§ 222 (Q) и упругое сопротивление системы также учитывается силой инерции:-^-x»4-P-Q=-^-x»4-P1=-^-x» 4-c x=0. (35.23) g1g1 1g1, где x-координата, позволяющая полностью определить положение груза Q во время вибрации (например, см. рисунок). 590); P-общее упругое сопротивление системы при вибрации; P-Q = PX-
так называемая восстанавливающая сила (дополнительные упругие силы, возникающие в системе в результате перемещения точки Людмила Фирмаль
приложения нагрузки Q на расстояние x при вибрации), координата x в пределах упругой (Pt=CX)\C пропорционально C. Решение уравнения (35.23) приводит к такой формуле для вычисления частоты o) 0 и периода свободных колебаний/0: Свободная вибрация невесомого тела, частота (период), длина равной частоты (периода) — это простая гармоническая вибрация с вибрацией математического маятника, равной статическому отклонению от нагрузки Q., Поддерживает нагрузку Q в середине пролета при изгибе балки на двух шарнирах И так далее. B. Если упругая система действует в одном направлении, то помимо нагрузки Q и упругого сопротивления системы P периодически изменяется возмущающая
Сила 5 и сопротивление среды R (35.24)690 с учетом силы инерции и вибрации[гл. XXXV Сопротивление действительной среды в случае значительного числа можно считать пропорциональным начальной степени скорости колебательного движения, т. е. r=rx»»сила интерференции 5 пропорциональна правильной скорости.: -х д-р х-с х=ч греха со/г*1 Или x «Sax’=s в(35.25), где n=^- так называемый коэффициент демпфирования колебаний, co0-частота свободных
колебаний указанных систем, возникающая при отсутствии как возмущающей силы 5, так и силы сопротивления R. Решение уравнения(35.25) приводит к такому выражению для амплитуды а вынужденных колебаний при наличии сопротивления: Двадцать шесть) — Статическая деформация системы от максимума мешающей силы 5 (Smsix=а). Отношение амплитуды вынужденных колебаний а к величине деформации называется коэффициентом нарастания
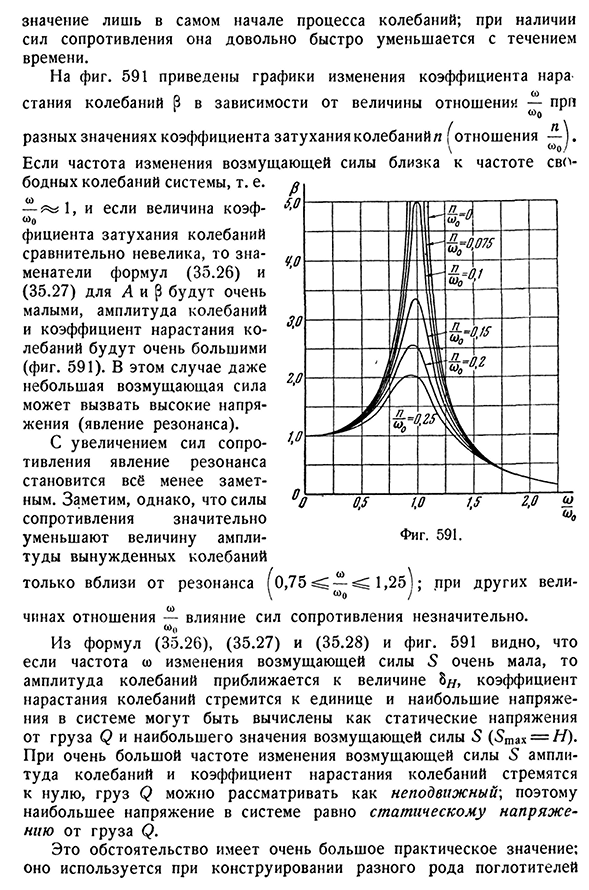
колебаний л.: (35.27) Таким образом, уравнение для динамического коэффициента(35.21) имеет следующий вид: ^ = 1 + ^ = 1 + — ^ 4 (35.28) Максимальная°С Эта формула не учитывает амплитуду собственных колебаний системы, поэтому важно рассчитать напряжение в [222]колебаниях 691 При наличии сопротивления оно довольно быстро уменьшается с течением времени. Как использовать 591 график изменения коэффициента демпфирования вибрации представляет собой график изменения коэффициента демпфирования вибрации B по его значению-для различных значений коэффициента
демпфирования вибрации n в g (отношение-j. Если частота изменения возмущающей силы близка к частоте свободного колебания системы, т. е. — ^1, а значение коэф<o Ноль. г Коэффициент демпфирования колебаний относительно невелик, знаменатели формул А и Р (35.26) и(35.27) очень малы, а амплитуды колебаний и коэффициенты нарастания колебаний очень велики (рис. 591). В этом случае даже небольшая мешающая сила может вызвать высокое напряжение (явление резонанса). По мере увеличения силы
сопротивления явление резонанса становится менее заметным. Однако следует отметить, что сила сопротивления существенно уменьшает величину амплитуды вынужденных колебаний вблизи резонанса при других значениях коэффициента-влияние силы сопротивления незначительно. <О0 Формула(35.26),(35.27),(35.28), Рис. Если частота W изменения 591 неугомонной силы S очень мала, то при приближении амплитуды колебаний к значению 8я коэффициент нарастания колебаний стремится совпадать, и максимальное напряжение в системе уменьшается. При очень
высокой частоте неугомонной силы 5 амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, так как нагрузку Q можно считать стационарной. Он используется в конструкции различных типов абсорбента 692, учитывающих силы инерции и вибрации. XXXV Вибрационные, сейсмографические, вибрографические и другие приборы. В машиностроении выбирают амортизатор, который защищает основание машины от сил, возникающих при вибрации, а частота собственных колебаний машины на амортизаторе определяется степенью силы заклинивания.
Смотрите также:
| Диск равного сопротивления | Учёт массы упругой системы при колебаниях. |
| Влияние резонанса на величину напряжений | Напряжение при ударе. Основные положения |

