Оглавление:





Вычисление напряжении от изгибающего момента.
- Расчет напряжения изгибающего момента. Изгибающий момент L4 может быть уравновешен только нормальным напряжением в виде прямой балки, а задача нахождения закона и формулы распределения напряжений на рабочей плоскости внешней силы, противоположной направлению, и для тех расчетов, которые больше момента L4, необходима и неопределенна для статики, необходимо
изучить изгиб мы опускаем такие расчеты при определении напряжения,§ 187] расчет напряжения от изгибающего момента 585 Поскольку вы уже используете готовое решение, необходимо учитывать нормальное напряжение балансировки изгибающего момента 7I, которое описано при определении
вертикального напряжения прямоугольной балки. Рассмотрим равновесное Людмила Фирмаль
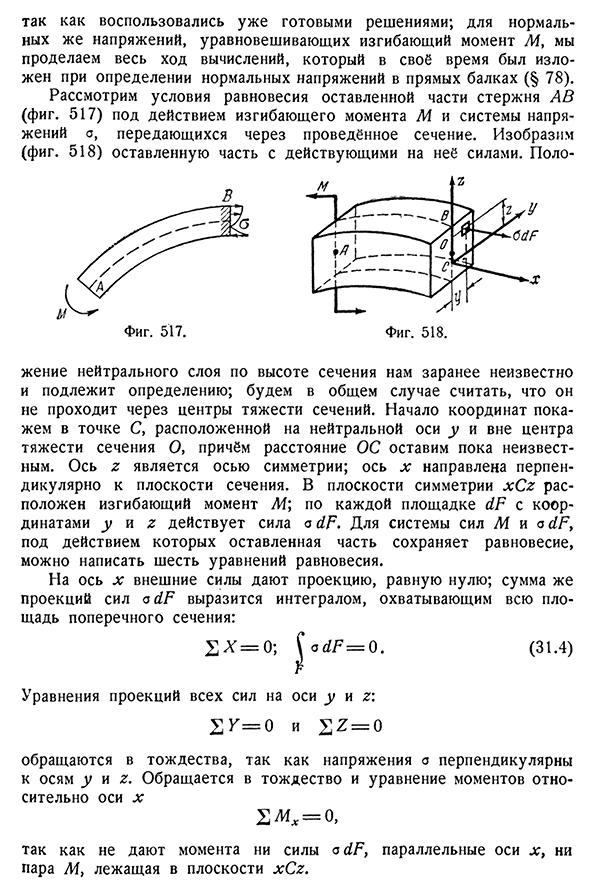
состояние левой части стержня АВ (рис. 517) передача через секции производится под действием изгибающего момента M и напряжения системы o. Нарисуйте (рис. 518) левая часть с действующей на нее силой. Поло- Фигура. 517 рис. Пятьсот восемнадцать Расположение нейтрального слоя на высоте поперечного сечения нам заранее не известно и подлежит определению. Начало координат появляется в точке C, расположенной вне центра тяжести на нейтральной оси
y и участке O, а расстояние до оси остается неизвестным. Ось Z является осью симметрии, а ось x перпендикулярна плоскости поперечного сечения. Плоскость симметрии xC z имеет изгибающий момент M. Для системы сил M и o dF можно записать шесть уравнений равновесия под действием левой части, удерживающей равновесие. Внешняя сила дает проекцию, равную нулю; сумма
- проекции силы dF представляется интегралом, охватывающим всю площадь поперечного сечения:^X=0;^d F=0. (31.4) Уравнение проекции всех сил на ось Y и ось z:% Y=0 и S-Z=0 становится одинаковым, поскольку напряжение o перпендикулярно оси y и оси Z.%M x = 0, потому что ни сила adF, параллельная оси x, ни пара L4 в плоскости xcz не дают момента.586 криволинейный стержень[глава XXXI по той же причине момент VS L4 относительно оси z также равен нулю; для силы adF эти моменты относительно этой оси являются
интегральными adFy. (31.5) Однако этот Интеграл равен нулю из-за симметрии поперечного сечения относительно оси Z. Остается обнулить сумму моментов всех сил относительно оси Y. Это уравнение записывается как^m y=0 -, M — \adFz=0. Ф (31.6) Поэтому в условиях статики необходимо рассматривать два уравнения: Если AdF = 0, Но (31.4) М — ^Д Ф з=0. Ф (31.6) Закон изменения нормального напряжения оставался неизвестным.
Это подводит нас к высоте раздела для рассмотрения Ворота возникают Это деформация. Для Людмила Фирмаль
случая изгиба прямого стержня используют гипотезу плоского поперечного сечения, которая подтверждается экспериментами и криволинейными стержнями. Будем считать, что под действием сечения, перпендикулярного изгибающему моменту \ оси, я остаюсь плоским и повторяю только одно за другим(рис. 519). Поскольку, согласно приведенному выше предположению(§ 184), ось балки остается в той же плоскости во время деформации, которую она ставит перед деформацией, вокруг этих po-нейтральных осей QCI и C2C2, напряжение на волокнах, разнесенных на одинаковое расстояние от оси, перпендикулярной внешней силе, а затем растянутых и укороченных, таким образом, становится одинаковым по ширине отношения между относительным углом поворота двух соседних участков и деформацией волокна, уточняется. Выберите
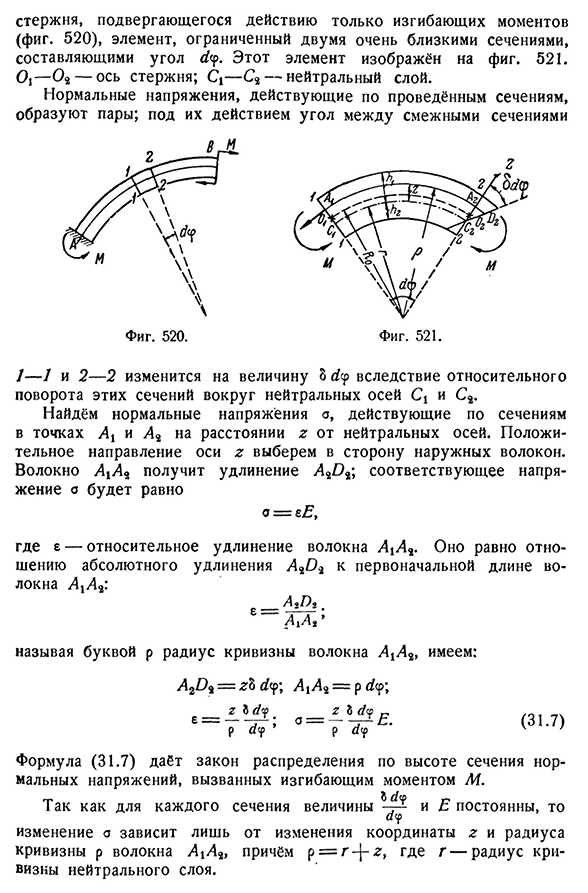
из кривой§ 187] расчет напряжения от изгибающего момента 587 Изгибающий момент (рис. 520), два очень близких сечения ограниченных элементов, которые составляют угол rfcp. Этот элемент показан на рисунке. 521 01-О2-ось стержня; — С2-нейтральный слой. Нормальное напряжение, действующее на пару проводимых секционных форм; угол между соседними секциями под действием 7-7 и 2-2 изменяются на величину 3dy за счет относительного вращения этих участков вокруг нейтральных осей CX и C2. Найдем нормальное напряжение o, действующее на сечение точек Ai и D2 на расстоянии z от нейтральной оси. Положительное направление оси Z выбирается
в направлении внешнего волокна. Волокно L1L2 получает удлинение L2T) 2;соответствующее напряжение a равно ми£, Здесь e-удлинение волокна D L2. Он равен абсолютному отношению удлинения D2O2 к исходной длине волокна^jX2: _2^2, Один Радиус кривизны волокна, называемого буквой p A i a Где M-изгибающий момент, а Интеграл охватывает всю площадь поперечного сечения. Интегралы, входящие в это уравнение, преобразуются следующим образом: зд Ф=^З Д Ф-Р^Д Ф F F F Последний из двух полученных интегралов равен нулю на основании (31.8), первый-это статический отрезок S площади поперечного сечения относительно нейтральной оси. Это значение
может быть вычислено как расстояние от его центра тяжести до нейтральной оси, то есть произведение площади поперечного сечения F на z^. 522): С=ФЗ*. (31.11)поэтому уравнение (31.10) принимает вид: И так оно и есть. Я^Ы=М; Б dy _ м~Д^~Е> (31.12) (31.13) И формулы для нормальных напряжений записывается следующим образом: Зет_ — • п (31.14) В Формуле (31.12) здесь мы находим, что статический момент S площади поперечного сечения относительно нейтральной оси не равен нулю, то есть поперечному сечению, когда нейтральная ось изгибает изогнутый стержень. 522 мы нарисовали этот сдвиг к центру кривизны стержня. Результат определения
величины g по формуле для различных сечений (31.9) показывает, что нейтральная ось фактически движется в указанном направлении. Это смещение обусловлено условиями равенства суммы сжимающих и растягивающих напряжений, действующих на поперечное сечение. Потому что напряжение от изгибающего момента на внешней кромке сечения невелико, а на внутренней-больше, чем на соответствующих волокнах прямого стержня того же сечения (рис. 522), для равенства указанной суммы нейтральная ось должна быть смещена от центра тяжести сечения к внутреннему волокну.590 изогнутый стержень[гл.
XXXI В дополнение к полученному напряжению мы получаем формулу для вычисления полного нормального напряжения изогнутого стержня, применяя напряжение, замеченное в предыдущем пункте, от вертикальной силы: (31.15)) Максимальные растягивающие и сжимающие напряжения абсолютной величины находятся в крайних волокнах 1 и 2(рис. Пятьсот двадцать два),
Смотрите также:

