Оглавление:



Вычисление моментов инерции сложных фигур
- Расчет момента инерции Сложная иллюстрация При расчете разных балок необходимо определить момент инерции сложного сечения.
Для практических расчетов необходимо разделить сложную фигуру на простейшую и рассчитать момент инерции для каждой рассматриваемой оси.
Расчет начинается с определения центроида Людмила Фирмаль
всей фигуры относительно произвольной системы координат. Рассмотрим пример определения момента инерции, показанный на рисунке. Это 163. Возьмите ось с OTA * в качестве первой оси.
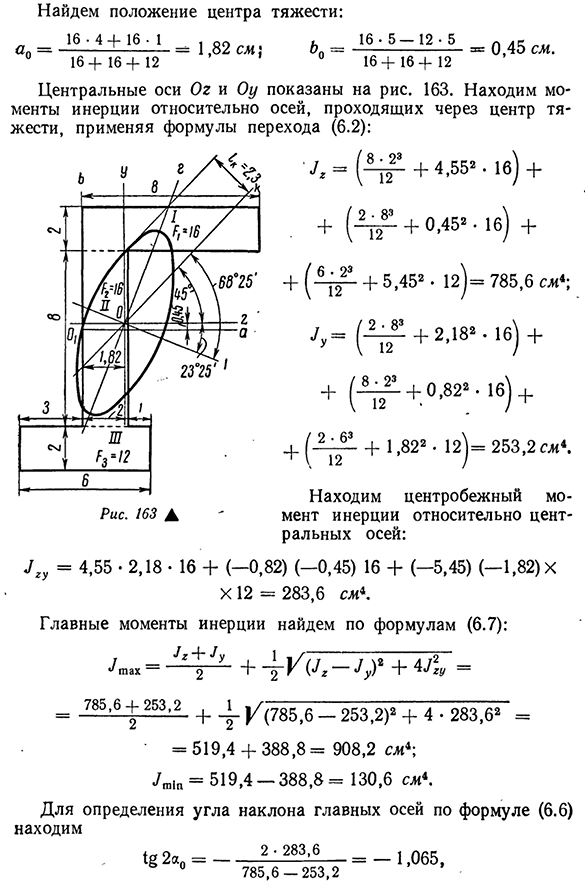
Разделим фигуру на три прямоугольника: /, 11,111. история * Ось (\ a проходит через центр тяжести второго прямоугольника. 181Найдем положение центра тяжести: 16 • 4 4 -1 6 • 1 16 4-16 16-12 = 1,82 см; 1 6-5 —
- 1 2 -5 16 4-16 16-12 = 0,45 см Центральные оси Og и OU показаны на рисунке. 163, используйте формулу перехода (6.2), чтобы найти момент инерции относительно оси, проходящей через центр тяжести): J = (-PG- + 4’552 • 16) + + (AG * + ° 452 • 16) + + (-l g- + 5 -4 5 2 ‘1 2) = 7 8 5 -6 СМ i-J, = + 2,18 * • 1 b) + + (- ^ — + 0,82 *. 1B) + + (AG «+ 1,822 ’12) =
253’2 6 _ 253,2) 2 + 4,283,62 = = 519,4 4-388,8 = 908,2 см \ LPS = 519,4-388,8 = 130,6 см *. Чтобы определить угол наклона главной оси согласно уравнению (6.6), tg2a0 = — 2-283.6 785.6-253.2 = -1,065, Противоречивые 182, 2a0 = -46 ° 5 ‘и 0 = -23 ° 25’. Угол A0 указывает положение шпинделя, где момент инерции имеет максимальное значение,
когда Jz> Ju, и минимальное значение, когда JZЛюдмила Фирмаль
оси инерций 1 и 2 показаны на рисунке. Найти 163 радиуса инерции: 1 / 908,2. — // 130.6. ^ tah u44 4.54Cmt ^ min- | / 44 — 1 «72CM. Согласно этим данным построен эллипс инерции (рис. 163).
Смотрите также:

