Оглавление:






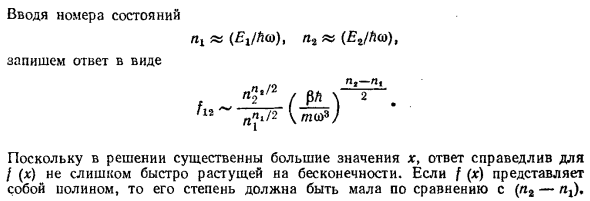

Вычисление квазиклассических матричных элементов
- Квазиклассический расчет Матричные элементы Прямой расчет матричных элементов Использовать физическую величину / полуклассическую волну Новые функции идут с большими трудностями. Заранее Энергия состояния перехода между 1) Пройдите по нижней полуплоскости и определитесь с A Неправильно, потому что рядом с секцией пути (-7r <(p <-7r / 2).
- Крайний левый (φ задается уравнением (2)), член exp (r £ 2/2) экспоненциально Очень маленький по сравнению с терминами, содержащими exp (-r £ 2/2). § 51W H I S L E N I E K A ZI K L A S S I C H E S K I X E L E M E N T O V 233 Поскольку матричные элементы рассчитываются не близко друг к другу, Последнее не сводится к фурье-компоненте / (§48). Сложность связана с тем, что lu экспонента (большое мнимое число Свойства экспоненциальных волновых функций Срок, интеграция Быстро вибрирует Ной.
Рассмотрим одно измерение Кейс (движение поля U (x)) и Для простоты оператор фи Физическая величина / это просто функция. Людмила Фирмаль
Координата х. u> 2 волна Новые функции, которые соответствуют некоторым Значения энергии частиц E1 и E E1 Рисунок 17); Предположим, что ^ 2 действительно выбран. мы Вам нужно рассчитать интеграл + оо Рисунок 17 / 1 2 — Я ip iffodx. (51,1) Согласно (47.5) волновая функция области с обеих сторон Дрон с поворотной точки х = а \ (достаточно далеко) Имеет форму = и ехр / 1 для х> а \ (51,2)
То же самое верно для φ> 2 (замените индекс 1 на индекс 2). Однако интеграл (51.1) вычисляется по следующей подстановке Он из этих асимптотических выражений волновых функций Даст неправильные результаты. Факт, как мы видим Ниже этот интеграл экспоненциально мал Ранг, интегрировать себя Не маленький.
Поэтому последнее сравнительно небольшое изменение Вообще говоря, измените порядок величины интегрирования. Это Трудностей можно избежать следующим образом: Функция φ> 2 выражается в виде суммы φ> 2 = Ф2 + ‘Ф2>. Косинус жив (с областью х> 0,2) суммой двух экспоненциальных функций 234 K V A ZI K L A S S I C H E S K I Y S L U W A H H. VII Формула.
Согласно (50.2) / + -1C2 Н / г — R EXP2Y / S V> 2+ = С2 2uf2 ехр Когда X CL2] (51,3) Функция ^ 2 является комплексным сопряжением = (V ^) *] Интеграл (51.1) также делится на сумму двух комплексных чисел Сопряженный интеграл, / 1 2 = + / 1 2> расчет Сделай это Во-первых, интеграция + оо / 1 2 = J V’l / V, 2_ Converge.
Конечно, функция области x \ p2 ) — рассматривать х-координаты как сложные переходы Установите переменную и установите путь интегрирования от реальной оси Верхняя половина плоскости. когда х становится положительным В моем приращении появляется функция (область x> a ) Увеличивайте количество участников, но уменьшайте функции быстрее.
В области x> a \ везде есть p 2> p . Поэтому до Зернистое выражение уменьшено. Предвзятый путь интеграции не проходит Точка x = a i, a 2 на вещественной оси, квази-квази Классическое приближение не применимо. Так все время Доступные функции Асимптотическая формула в верхней полуплоскости.
Это Есть функция = F2 = С1 2 [2 м (U-i? I)] 1/4 опыта -i C 2 2 [2 м {U-E 2)] 1/4 опыта ‘R \ ± J y / 2 м (U-E j d x l 4 аи — ~ N j y / 2m {U-E 2) d x \ (51,4) a2 Где корень определяется на реальной оси региона х <и они положительные. С интегральной d = i S r / e x p (; / «Ag а2 ‘ Мы поставили перед собой цель изменить способ интеграции Таким образом, что уменьшает экспоненциальную функцию Мультипликатор.
Экспоненты имеют крайности только в следующих направлениях: U (x) = o (E \ φE 2, производная по x Не исчезнет в других точках Car). Поэтому смещение интегральной схемы Верхняя полуплоскость ограничена Нужно только обходить специальные точки> ч Функция U (x) \ Общая линейная теория Дифференциальное уравнение, которое они соответствуют _ — ^ x Особая точка волновой функции φ (χ) Конкретный выбор схемы зависит от конкретного рисунка 18 Поля U (x).
Следовательно, функция U (x) Половина из этого есть только одна особенность х = х0, то Пометка может быть сделана вдоль пути выше 18 типов. Основная роль интеграции напрямую Поскольку он находится вблизи особенности, целевой элемент матрицы ment / 1 2 = 2 Re fy 2 в основном пропорционально показателю степени
- Небольшое выражение, которое можно выразить как Хохо Я г / 1 2 до опыта j V 2 t (E 2-U) дх-J l / 2 т (E 1-U) дх (51,6) (JI. D. Landau, 1932) x). Как нижний предел интеграции Вы можете выбрать любую точку в классически доступной области. Стиль: этот конкретный выбор явно не влияет на воображаемое число 1)
Асимптотические выражения являются законными Интеграция 18 схемы определения взята из того, что показано на рисунке Размер подынтегрального, и, следовательно, относительно Последнее небольшое изменение не оказывает существенного влияния на стоимость Это очень важно. 236 K V A ZI K L A S S I C H E S K I Y S L U W A H H. VII Часть интеграции.
Замена волновых функций, выполняемых при выводе (51.5) и (51.6) Людмила Фирмаль
Некоторые специальные функции U (x) Требуется как точка верхней полуплоскости, тогда (51.6) xq Выберите тот, который имеет наименьшее абсолютное значение показателя степени Значение лютни value1). Уравнение (51.6) показывает, что энергии E1 и E2 В зависимости от результата матричные элементы достаточно близки, чтобы их можно было уменьшить.
Фурье-компонента времени классической величины f [x (t) . я? Предполагая 2, расширим с i = E = b, ( хо \ -w 2ilm J J ™ и dx j = exp (-w 2ilm t). (51,6 а) значение XQ XQ =! ^ ‘’ Ьь =! дх V (X) Можно рассматривать как сложное время частей tsa достигает точки x $ в комплексной плоскости x. (Значение v (x) = yj (2 (U-E (x))) / m — соответствующее «комплексное число Легко убедиться, что () (51.6a) определенно Дайте приближение к компоненте Фурье f [x (t) \ UJ21 Im t 1 предоставляется.
Квазиклассические матричные элементы Движение центрального поля симметрии Так же. Но под C / (r) теперь нужно понимать Потенциальная энергия (потенциал плюс центр (Энергия) и I значения разные Она будет другой. Имея в виду больше приложений Напишите действительную возможность предложенного метода Энергия двух состояний в общем виде, таких как U \ (r) И С / 2 (г).
Тогда, Целочисленное выражение (51.5) не имеет экстремального значения. Только в точке, где U \ (r) или C / 2 (r) меняется на бесконечность Не только нос, А 2 (г) -и 1 (г) = E 2-E 1 (51,7) г) Предположим, что сама величина f (x) не имеет особенностей. Расчетное значение матричного элемента (51,6) составляет «Нормальная» величина предэкспоненциального множителя. унция
Конечно, ситуация возможна, потому что этот фактор необычайно мал Суть проблемы. Простейшим примером является f (x) = const. В этом случае Из-за ортогональности волновых функций матричные элементы равны нулю Это не видно из формулы (51.6). Следовательно, формула < H j ^ 2t (E 2-U2) d r-J l / 2t (E 1-U) дрдр (51,8) Из конкурирующих ценностей го, а не только один, Особые точки U \ (r) и C / 2 (r), а также корень уравнения (51.7).
Центральная симметрия также отличается в следующих точках. Интеграл по др (51.1) из О (Не из -os) + os: В этом отношении необходимо различать два случая. Если вы Интегральная формула является четной функцией от r, тогда Это исследование может быть официально распространено на весь регион. До + ос, поэтому отличий от предыдущего нет эм.
Этот случай может иметь место, когда U \ (r) и C / 2 (r) четны Функция r [U (-r) = U (r)]. Далее волновая функция Xi (r) и (V) является четной или нечетной функцией (см. § 21) x), и Функция f (r) также четная или нечетная, и произведение X1 / X2 Может быть даже. Если подынтегральная функция даже не (Во всяком случае, это происходит, когда C / (R) даже не Ноа), тогда начало пути интеграции нельзя сдвинуть От точки r = 0 до количества значений r, конкурирующих в (51,8)
Вы также должны включить значение go = 0. Z a z h 1. Вычислить квазиклассические матричные элементы ( Экспоненциальный множитель) поле U = Uoe to ax. Решение U (x) бесконечно только для x-y-oo. Поэтому введите (51,6) x0 = -oo. Может быть интегрирован + Распространение на oO. Два интеграла индивидуально На пределе — ой.
Итак, сначала рассчитайте в диапазоне от —x + Перейти к oo, затем перейти к пределу х-оо. В результате о 0 / 1 2 ~ e x p —— (V2-V- 1), x) Для четного U (r) радиальная волновая функция R (r) является четной (нечетной) Для четного (нечетного) /, маленького г (где R к г л). 238 K V A ZI K L A S S I C H E S K I Y S L U W A H H. VII Где Vi = y / 2 E i / m и V2 = y / bEh / mn — скорости частиц на бесконечности. (W-oo), если движение свободно, 2.
То же самое для кулоновского поля U = a / g перехода между состояниями с / = 0. Единственная особенность решающей функции U (r) ка р = 0. Соответствующий интеграл был вычислен в вопросе 2 §50. В результате Получается по формуле (51.8) „G 7ha (1 1 И S ~ Exp-I ———— P \ V2 Vi, 3. То же самое для ангармонических генераторов с потенциальной энергией U (x) = 7 ^ x 2 + [3×4 Цель из Hs <& E1: E 2 <(1)
Решение: Обобщение на случай компактной поддержки вывода в тексте. Это движение показывает, что уравнение (51.6) все еще действует. В любом В качестве x0 вам нужно выбрать точку x-y = b °. Оба способствуют одному Заказать. У нас есть / -oo —OO \ / 1 2 до опыта (-i / s / 2 м (U-E2) dx-Jy / 2 м (U-Ei) dx1 j. а 2 а л В условии (1) основной вклад вносит регион y mcj y mcj 1 «m / ^ (2)
В этом ^ x 2 »E r, E 2, p x 4. (E i ^ / U) показатель степени (и нулевой член) Заказ будет уменьшен), игнорируя 3/3, (E 2 [d \ x \ Er f d \ x \ \ Логарифмические интегралы дивергенции должны быть усечены на границах Область (2), то есть x ~ ^ / (thio2) / 3 и x ~ 0.2 ~ y / E2 / (thio2) сверху От x ~ ai ~ y j E \ / (too2) и ниже. В результате / E 2, t 2io4 Ei t 2io4 / 1 2 ~ exp — In —— h-In 2No f3E2 2No p E g
Введите государственный номер rii «Ei / Ni, P2-E2 / fiw, Пожалуйста, напишите ответ в форме n ”2/2 / rp 4 (n2” ni) / 2 / l2 ~ n? л / 2 м 3 §52В Е Р О Й Т Н О С Т У П Е Р Е Х О Д А В К В А ЗИ К Л А Ц Ответ действителен, потому что большие значения х важны в решении. В случае / (g) он не очень быстро растет на бесконечности. Когда f (x) предварительно Является полиномом и его степень должна быть небольшой по сравнению С (n2-Pg).
Смотрите также:
| Квазиклассическое движение в центрально-симметричном поле | Вероятность перехода в квазиклассическом случае |
| Прохождение через потенциальный барьер | Переходы под влиянием адиабатических возмущений |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

