Оглавление:



Вычисление крутящих моментов и построение их эпюр
- Расчет крутящего момента И строительство их участка Нормальная сила, изгибающий момент и боковая сила равны нулю. Многие части машин и конструкций подвержены поворотам, таким как валы двигателя и машины, оси автомобилей и локомотивов, а также
элементы пространственной структуры. Помимо скручивания, механические и конструкционные элементы иногда испытывают изгиб или сжатие. Такие случаи изучаются в главе XI, где рассматривается только один поворот.
Исследования показали, что характер деформации витого стержня сильно зависит от его формы Людмила Фирмаль
поперечного сечения. Среди стержней с различными поперечными сечениями, которые подвергаются кручению, специальные места занимают стержни с наиболее распространенными круглыми или круглыми поперечными сечениями в данной области техники.
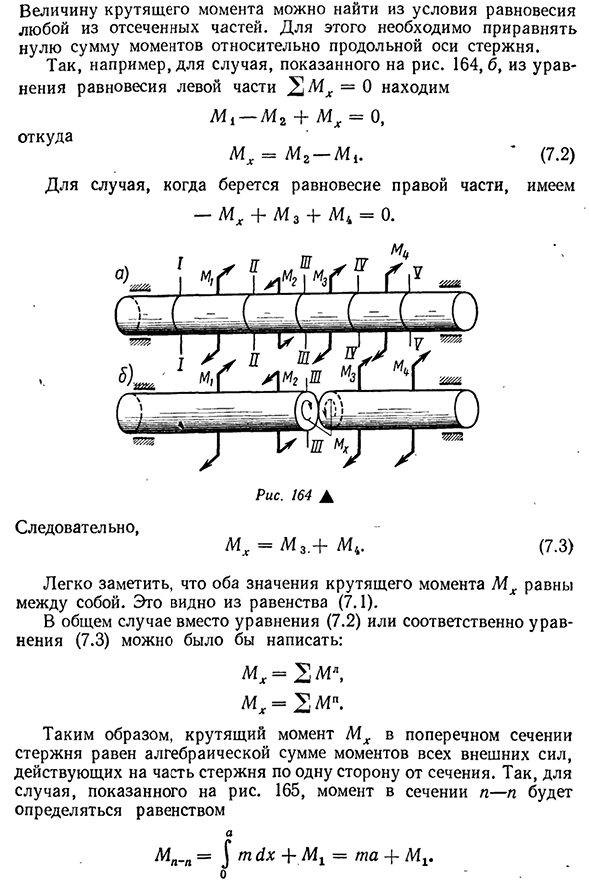
Несколько внешних времен могут быть добавлены к витым стержням в разных разделах. Рассмотрим случай, когда все внешние моменты уравновешены друг с другом и действуют на плоскости, перпендикулярной оси стержня (рис. 164, а): Mi-M2 + M3 4-M4 = 0. (7.1) Чтобы определить крутящий момент в любой секции, например I I-III,
- мысленно разрезайте вал в этой секции на две части и каждую часть крутящего момента MX <84 Значение крутящего момента может быть получено из любого равновесного состояния обрезанных частей. Для этого сумма моментов вокруг продольной оси стержня должна быть равна нулю. Таким образом, например, как показано на рисунке. Из уравнения равновесия в левой части 164, b, 2 ^ x «0 находим L41-M2 +
MX-O, Откуда MX = M2-M1. К (7.2)) Если правая часть сбалансирована, она имеет -MX- | -MzT «= 0. Рис 164А Следовательно, L4X = M3. + Afj. (7.3) Легко видеть, что оба значения крутящего момента M x равны друг другу. Это ясно из равенства (7.1). В общем, вместо уравнения (7.2) или уравнения (7.3): m x = 2 мл, = 2 мегапикселя. Таким образом, крутящий момент MX в поперечном сечении стержня равен алгебраической сумме моментов всех внешних сил, действующих на участок стержня с одной стороны сечения.
Поэтому будет описан случай, показанный на фигуре. 165, сечение р-р момента определяется равенством но Людмила Фирмаль
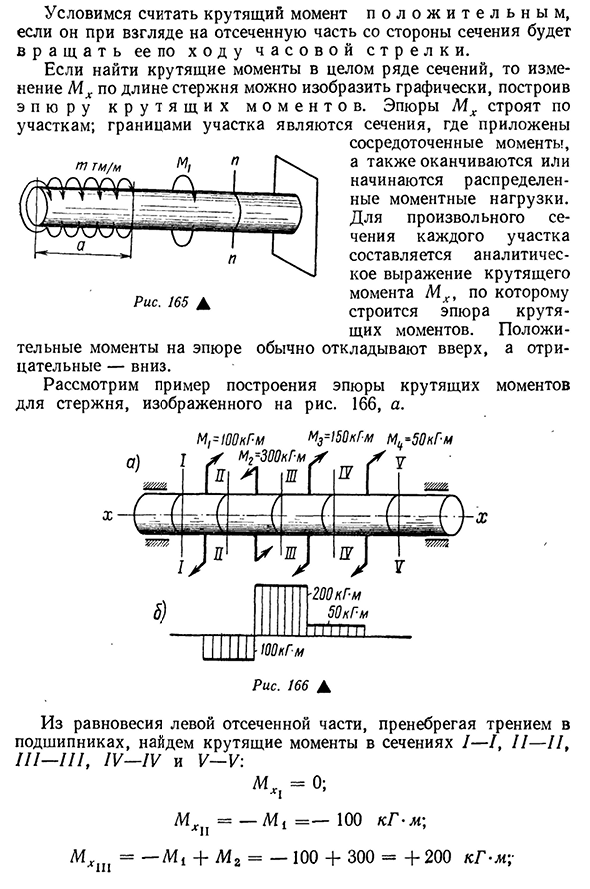
Мегапиксельная p = J m dx + = TA + A4X.o-. 185 страниц 165А Согласитесь учитывать момент затяжки и обороты при взгляде на отрезанную часть со стороны секции. Если вы найдете крутящий момент в нескольких разделах, вы можете графически изобразить изменение MX по длине стержня. График M x построен в секциях, границы секций добавляются при применении сосредоточенного времени, а также в секциях с распределенной нагрузкой крутящего момента, превышающей или запускающей Для любого сечения каждого сечения собирается аналитическое представление крутящего момента MX, и соответственно строится график фактического момента, а последний на графике Рассмотрим пример построения графика крутящего момента штока, как показано. 166а Twist —
поставил — и — отрицание — момент Не обращая внимания на трение подшипника, найдите моменты затяжки в секциях / —I, I I-II, I I I-III, IV-IV и V-V из баланса левой отсечной части: W = 0; Mxx n = -M i1 = -100 кг-м; Mxx = -Mi + M2 = -100 + 300 = + 200 кг-м; 186ML {y = -M i + M2-M3 = — 100 + 300— 150 = + 50 KL l; MXy = -M i + M2-M3-M i = — 100 + 300— 150—50 = 0. Из этих уравнений видно, что крутящий момент в каждой секции постоянен. Участок M x показан на рисунке. 166b В качестве второго примера рассмотрим график крутящего момента штока, показанного на рисунке. 167, а. При построении графика M x учитывается равновесие правой части отсечения. В этом случае момент реакции уплотнения не может быть рассчитан. Секция крутящего момента х \ Будет: I-я I I-II M xX II — M i = -40 кг-л; I II-H I MX w = -M i + M2 = -40 + 70 = + 30 кг-М-, IV-IV M. IV = — + М2-М3 = — 40 + 70—50 = — 20 кг-м График крутящего момента M x показан на рисунке. 167 б
Смотрите также:

