Оглавление:






Вычисление коэффициента жесткости восстанавливающей силы при конечных перемещениях
- Для определения восстанавливающей силы во время заключительной операции рекомендуется следующая процедура. 1 Определить положение равновесия неподвижных точек с помощью пружины. Это дает конечное смещение точки в направлении, необходимом для нахождения обобщенного коэффициента жесткости. 3 Вычислить сумму проекции силы упругости в направлении движения. Это и есть желаемая восстанавливающая сила.
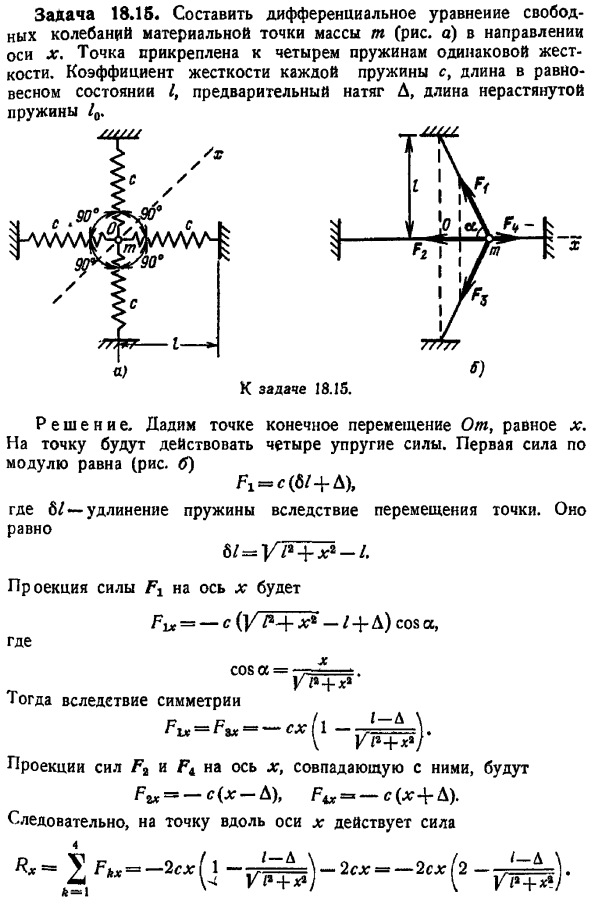
Найти обобщенный коэффициент жесткости путем вычисления производной восстанавливающей силы по отношению к перемешиванию. Задание 18. 15. Создайте дифференциальное уравнение для свободных колебаний в направлении оси x материальной точки массы m рисунок а. Точка прикреплена к 4 пружинам одинаковой жесткости. Коэффициентом жесткости с каждой пружины, длина Эквилибриум я, натяг Д, длина не растягивая пружины. 10 Решение. Приведем точку с конечным смещением, равным x. 4 на точку действуют упругие силы. Абсолютное значение первой силы равно рисунок b Ф1 с а Где 6z-удлинение пружины за счет смещения точки.
Внешними называются силы, приложенные к материальным точкам рассматриваемой системы со стороны точек и тел, не входящих в состав этой системы. Людмила Фирмаль
И равны 61 гг ХД-1 Проекции силы fi. Тогда для симметрии проекция силы fa x, совпадающей с ними, равна — с х-Д, фто — с х Д. В результате сила действует на точки вдоль оси x Дифференциальное уравнение для точечной вибрации имеет вид Представление о напряженном состоянии системы в заданном направлении можно получить из производной силы перемещения, которую также можно назвать коэффициентом жесткости данного положения. Конечно, в этом случае восстанавливающая сила не равна СХ. Найдем обобщенный коэффициент жесткости в направлении оси x. Один П СГ ЛГ В этом случае обобщенный коэффициент жесткости является функцией перемещения. Задание 18. 16.
В условиях предыдущей задачи определите восстанавливающую силу при конечном смещении точек вдоль оси x. И По вопросу 18. 18. Ось x n lt вдвое уменьшает угол между соседними пружинами. Решение. Дайте точке смещение om x вдоль оси см. Рисунок и определите силу, действующую на точку, учитывая, что все пружины растянуты. Тогда, коэффициент упругой силы Р1 Р1 З Д 1 Д Где d x-удлинение соответствующей пружины, вызванное смещением точки om. Д х ам-а о Г — 2 На zx-. Из треугольника oam используйте теорему Косинуса, чтобы найти p z x — 2 1x x −2 y x-y2 zx x cos a, откуда. 2х в21 потому что А — Р — — — — — — — — -. 2ur х — У2 х И затем.
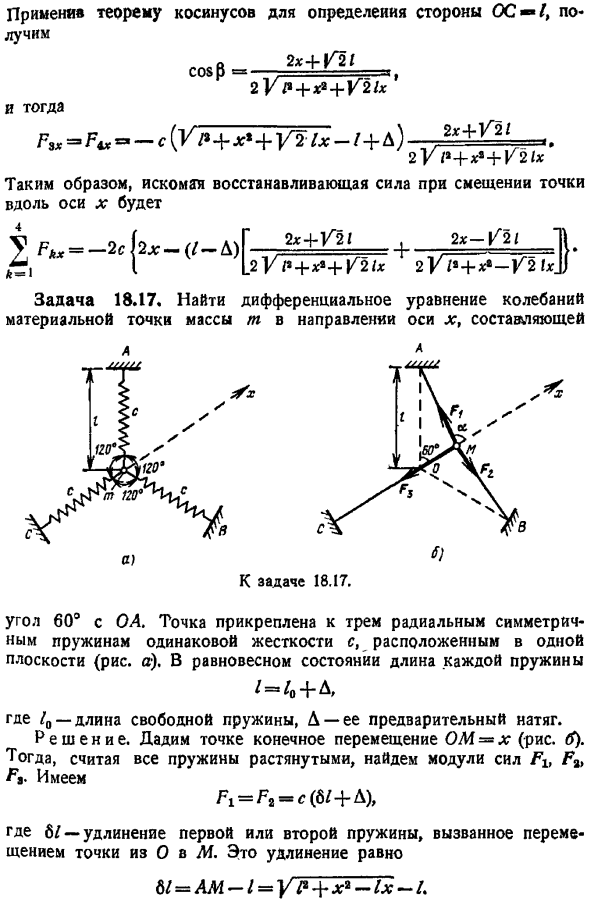
Аналогично, из треугольника COM См г 4 У2 х. Примените теорему Косинуса для определения стороны OC Z .д 2х Y21, потому что п, 2UR х y21x И затем -с г 1 х Y21x-1 ГХ 1 2У П Y21x Таким образом, требуемая восстанавливающая сила при смещении точки вдоль оси x равна U 2х — 21-П 2У Х2-К2 fxJJ Задание 18.17.Найти компонент дифференциального уравнения колебаний по оси Х массы m точки масс По вопросу 18.17.OA и угол 60.Эта точка прикреплена к 3 радиально-симметричным пружинам с одинаковой жесткостью c в одной плоскости рис. а. в равновесии длина каждой пружины равна З Z04-А Zo-длина свободной пружины, А D-ее преднатяг. Решение.
Дадим точке конечное смещение OM x рисунок B. Далее, учитывая все растянутые пружины, находим коэффициент силы Flt F Ft .У нас есть Где 6Z-удлинение первой или второй пружины, вызванное смещением точки от O до M .это удлинение равно 6Z АМ −1 ВФ х — на ZX −1 Если мы применим теорему Косинуса к стороне OA треугольника OAM Р М Фра 2АМ ом со а откуда Р ХС-1х х 2х Г П Х1-ЛК потому что, потому что а —1 2х -, 2UR х −1х Проекция силы Ft или F на ось x равна Исправить Фу с УР х- х −1 Д Проекция мощности Fa на ось x равна ПВ — — — Д.
- Затем дифференциальное уравнение колебаний вдоль оси X. Вы будете. Или наконец-то tl- ОМК Дж л-2 раза Ви х — ZxJ. Кроме того, вычисляя производную Rx по координатам x, мы находим обобщенный коэффициент жесткости. Ся — Зе 1 ——— 2 −1, 5. Задача 18.18. Задача 18 17 исследует неоднородность упругого поля системы. Это конечное, малое смещение точки в любом направлении в плоскости пружины. Решение. Рассмотрим упругое поле системы в случае конечного перемещения. Дайте точке m конечное смещение O x в любом направлении Ox .Затем восстанавливающая сила Fx действует на точку m и направляется в точку O, являющуюся положением равновесия рис.
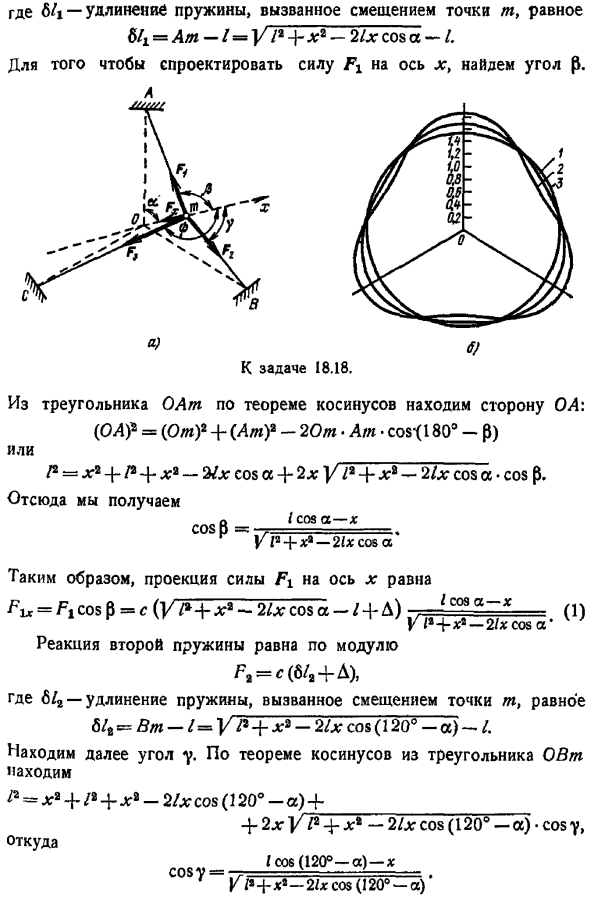
Чтобы найти эту силу, мы поступаем следующим образом находим реакции каждой из 3 пружин FBF Fa и проецируем эти силы в направлении оси X. Это будет желаемая сила Fx .Оси Ox образуют начальное направление пружины OA и угол, A, а также угол между направлением пружины и осью Ox после смещения соответственно 0, y, рисунок A .Отклик первой пружины по модулю равен Д1 с 64 Д Здесь Mi-удлинение пружины за счет смещения точки t .64 At −1 At Z x1-2 xcosa-I .чтобы спроецировать силу на ось x, найдите угол p .Т К выпуску 18.18.Из треугольника OAt, по теореме Косинуса, находим латеральный OD OD 8 From At — 20m Am cos- l 80 — P or P x P x −3 x cos a 2x Y l x — 2L XCOSA cos p .отсюда потому что Р.
Угол а, образуемый вертикальным направлением с экваториальной плоскостью, называется географической широтой в данной точке земной поверхности (см. Людмила Фирмаль
Коза Версия 12 — 21hsoea Таким образом, Проекция Силы 4 на ось x равна FICOs Р С Г х −2 xcosa- Д.— С А-Х.1 1 г х — 2lxcosa Отклик 2-й пружины равен по величине Г1 с 6 1 Д Где 61g-удлинение пружины, вызванное смесью точек m, равной 61.Б-у у B- -х −2lx вида COS 120 -а −1 Далее мы находим angle-y .By по теореме косинусов из треугольника О Ш P x x-2 xcos 120 — a 2 х у Х −2 xcos 120 -а, потому что Г, откуда 1 соя 120 — a — x уютно −7.— У — 21hc0z 12.
Проекция силы Ft на ось x равна Ф −2 х в COS 120 -а −1 Д х В — А и M120 — х А х — 21хсов 12. Аналогично, найдите 3-ю силу Fa c 6 A, где 6 8 г х — 2lx вида COS 120 а −1.Используйте теорему Косинуса, чтобы получить следующее c0s l2O a — С С Г Х2-2 xc0b 12O а И затем В FSX ФС со Ф С Г Ф Х-2lx в COS 120 а -я Д х В C0S архитектуры i2o а — х х −2 xc0s 120 а 1 2 3 Используйте A, чтобы найти восстанавливающую силу, которая стремится вернуть точку в положение равновесия F.
Уравнение приведенного коэффициента жесткости упругого поля в любой точке плоскости J найдено дифференцированием FX на X Е С-Ф Д Т- дх я 1 х — 21hs0vya 3 2Т, грех 120 грех 120 я Г P x — 2lx C0s 12b — i 3 2 l x −21xcos 120 a 3 2Jr I и имеют систему с конкретными значениями D, и в подставленном результирующем уравнении мы можем дать определенное значение x для угла a от 0 до 2 l и получить зависимую кривую a .на рисунке b полярная система координат c, a показывает 2 такие кривые для различных начальных помех D для одного и того же I и x .1 2, x 0, 1, d 0, z-кривая, 1.Кривая 1 2, x 0, 1, d 0, 2 2.Теперь рассмотрим упругое поле системы, когда смещение мало и отсутствует начальная интерференция.
Система состоит из 3 параллельное соединение Springs .To определите пониженный коэффициент жесткости, используя следующую формулу с — С С что а, я Где cn-коэффициент жесткости упругого поля в направлении оси x, ct-коэффициент жесткости n-й пружины, а a-угол между этой пружиной и осью X . Для рассматриваемой системы с с соз а соз 120 -а соз 120 а т.5 Так, в случае малых отклонений коэффициент жесткости приведенного поля не зависит от угла А. То есть вблизи положения равновесия упругое поле однородно. На рисунке b показан круг кривая 3 и показана зависимость c a от малых отклонений.
При наличии начального зажима можно найти уменьшение коэффициента жесткости в точке равновесия O и поместить смещение x 0 в Формулу 4. Сравнивая 5 и 6, мы видим, что начальная интерференция влияет на коэффициент жесткости упругого поля при малых перемещениях. B данные из 6 2, D 0, 1, при использовании для создания кривой на рисунке 1, 1 — л Это окружность с радиусом, превышающим 3 радиуса окружности 3 На рисунке 0.1. б.
Смотрите также:
Предмет теоретическая механика

