Оглавление:





Вычисление коэффициента жесткости при малых перемещениях
- Если смещение невелико, то обобщенный коэффициент жесткости определяется по следующей формуле 1. Для n пружин, которые установлены на корпусе и направлены под углом u относительно движения, соответственно. Где c-модуль жесткости пружины, и положение равновесия точки происходит в где c-модуль жесткости пружины. Эта формула справедлива и для небольшого смещения из положения равновесия. Если нет предварительного натяга пружины в положении равновесия. При последовательном соединении n пружин, действующих в одном направлении, обобщенный коэффициент жесткости получается по следующей формуле 2 мА 2. Кроме того, эта формула применима как к малым перемещениям, так и к конечным перемещениям.
После нахождения обобщенного коэффициента жесткости можно построить дифференциальные уравнения движения и определить частоту и период свободных колебаний. При решении задачи расчета обобщенного коэффициента жесткости при малом перемещении, составлении дифференциальных уравнений движения, определении частоты и периода колебаний, практически не следовала следующая последовательность действий. 1 определить положение равновесия точки под действием силы упругости. 2 придайте точке небольшое смещение в направлении, необходимом для определения коэффициента жесткости. 3 вычислить проекцию силы упругости, возникающей в результате перемещения точек в направлении движения.
Учитывая формулы (1) и (2), представим это уравнение так: или где обозначено: (3) Интегрирование затруднении: дифференциального уравнения (3) не продета в. Людмила Фирмаль
Найти обобщенный коэффициент жесткости и разделить сумму результатов проекции силы упругости на перемещении точки. б упростите результат, отбросив величины, превышающие наименьшую 1-ю. 6 Создайте дифференциальные уравнения движения системы. 7 определите частоту и период вибрации. Задание 18. 12. Жесткая пружина крепится к массе м По вопросу 18. 12. Длина пружины 0 без деформации. Определить обобщенный коэффициент жесткости пружины для малых перемещений точек вдоль оси x. Если вся система находится на горизонтальной поверхности, найдите частоту мелкоточечных колебаний. Решение. Выберите точку равновесия для точки за пределами начала координат o. Дайте точке небольшое смещение oa x.
Тогда пружина образует ось x и угол a, длина которого будет равна l. Модуль упругости равен Р с — 0. Эта сила направлена от a к oh рисунок b. Проекция этой силы в направлении движения — С — 0 СО8О. 1 смещение ОА определяется уравнением ОД — сова — 0соза0. 2 обобщенный коэффициент жесткости в направлении x равен c — c — x x С другой стороны, цифра должна быть b xso8a 0 sosba. 4 Но поскольку Ба-это небольшое 1-секундное небольшое количество, примерно Откуда Рис. 1, co8a sov a0-6a r co8a0 i-1a x ow a. 5 Если ввести это значение равным образом 3 СОЭ СХ А0 икс — В Сов8 6 Формула 1 является обобщением результата 6 в случае любого числа упругих связей, прикрепленных к точкам под разными углами.
- Создайте дифференциальное уравнение для изменения малой точки Тх — с cos1 А0 х Или Х х-О. Частота колебаний равна А cosa0 г Цикл вибрации Т 2л усл Т Задание 18. 13. Нагрузка на массу Т устанавливается на пружине согласно рисунку, приведенному на рисунке. 18. 2. Определите обобщенный коэффициент жесткости для незначительного перемещения нагрузки в направлении оси x. Составьте дифференциальное уравнение движения и определите частоту и период колебаний. Решение. Угол a относительно оси x.
Найти коэффициент жесткости пружины, эквивалентный 3 пружинам, действующим на g. 2 пружины, в которых коэффициенты cd и cr соединены параллельно, соответствуют 1 пружине коэффициента жесткости 1 c2 — — c2. So, в угловой ах имеются 2 пружины, соединенные последовательно с коэффициентом жесткости d-rcz, а коэффициент жесткости приведенной пружины равен 2 Откуда Да. а, н ы СА с ДР. С1 д д Затем определяют коэффициент жесткости приведенной пружины. Под углом А3 Откуда 2 Используйте следующую формулу 1, чтобы найти коэффициент жесткости приведенных пружин с небольшим смещением в основном направлении.
Разложим его на относительное по отношению к станине А и переносное (в данном случае поступательное) вместе со станиной. Людмила Фирмаль
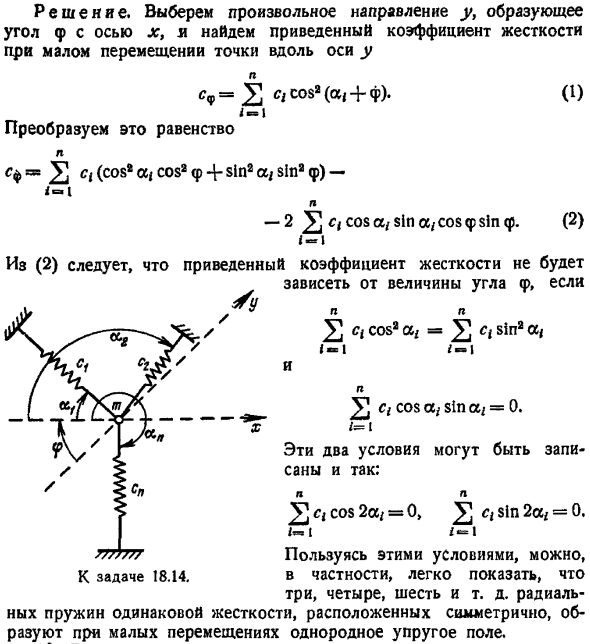
Ввел значения, найденные в этом уравнении 1 и 2, и далее рассматривая ca, — c3, наконец s s s s СО52 1 с 2 2 ykc08 З- Здесь az 270 и С050з 0. Дифференциальное уравнение для вариации малой точки имеет вид ТХ — СХХ Откуда берется частота колебаний Цикл вибрации р м 2 Задание 18. 14. Точка массы m находится в одной плоскости и образует соответствующий угол o x оси и угол o, а коэффициент жесткости c. В соотношении c1 и a радиальный обобщенный коэффициент жесткости одинаков для малых перемещений точек. Решение.
Выберите любое направление y, чтобы сформировать ось x и угол. Найти уменьшение коэффициента жесткости при малом смещении точек вдоль оси y СР г с co82 А Ф. Преобразование этого равенства н Сф УС С08 а С082ф4-81п2а 81paf — 1 Но. .−2УС СО8а, 81Па СО8ф81пф. 2 1 1 2 Из, для N p, приведенного коэффициента жесткости не зависит от значения угла.2с18282а 2C151naOS 1 −1 Ноль Может быть записан Для C 31n2a 0.г 1 Условие, может показать его н Г С потому что, s1n 0.Я — Я — Эти 2 условия Я не уверен, что это так.
Смотрите также:
Предмет теоретическая механика

