Оглавление:





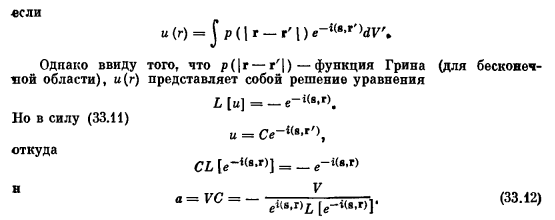

Вычисление флуктуаций величин, рассматриваемых как функции положения в пространстве
- Молекулярная структура. Если указано только деление на любое число домена b, то указывается номер функции. Я думаю, что мы можем описать только эту форму гауссовского распределения. |.) ОДВ… 1г. — Я /(2-й) -] -, » * — в ^ б…(СЗ.1 Здесь мы предполагаем, что среднее значение равно нулю. Обратите внимание на следующее: Dp / 0, Здесь Dp-это свободная энергия B, заданная.
Чтобы понять смысл такого определения вероятности, рассмотрим среднее значение ρ= 6vs, где справедлива теорема сложения вероятностей (33.1) и одновременно должно выполняться известное условие (поскольку оно полностью определяется гауссовским распределением).Эти (30.7) узнайте расположение и размер 2 областей We, P. = P(b, M. Предположим, что вы хотите разделить домен b. = B » + b. затем, к точке 5, в этой области、 п («***а Условие доли ₽= Р(6 * «а + д) Функция p (g, g) для различных объемов) B перейти к пределу-* 0, I ’ — * * 0; затем п(г, г’) — е(г)6(г’)- Мул. Вообще говоря, как вы видите ниже, » бесконечно.
Существование термического уравнения состояния вытекает из закона транзитивности термического равновесия. Людмила Фирмаль
В результате определяется неперекрывающиеся функции-2 DF / c эквивалент Dan: пространство данной функции! 2?= Р15.Е] ^,(33.5) Где [III, 6]-дифференциальная форма 2-го порядка. Обозначается E,£ / если дано, op- / ) Сначала завершите Etim, используя поток (так же, как это делается при выводе equation. It достаточно уметь рассчитать изменчивость*)). (33.6) 2-й Интеграл Площадь поверхности A. выражение 1 подоператор eile — ^ [E, _B]; — оператор,- — — — — — Это само-Ву / Жужу зеленый**) дифф «Для (E) граничного условия Y [E] — 0, соотношения (33.3), связи и pm, в различных формах следующим образом. Если… 2 ^(n, 5)= 2 • ) Например, Курант Р., Гильберт Д.
Метод математической физики — 3-е издание, — М.: Гостехиздат, 1951, Т. 1, гл. IV,§ 3. •• ) Там же, гл. В§ 10. (33.3) по (33.7) Эта связь сохраняется, V» — «0, V, — «’это выражение (33.6) 5 — p (r, H»»’)» Г 6 (г) 6 (Г) Д’. (33.8) Однако если p (r, r») является функцией Грина, то свойство(33.7)’) вызывает£[$®] — C ®и JV [fc] = 0 (на границе области).Следовательно, из (33.6) Получите соотношение, которое вам нужно.
- Если, как это часто бывает, влияние границ тела незначительно, то в этих случаях можно взять функцию Грина бесконечного оператора L [J]. Полученные результаты позволяют дать следующую интерпретацию рН (аналогичную приведенной в§ 16), Если£является функцией, характеризующей состав тела (например, компонент перемещения частиц в твердых телах). Условие статического равновесия, когда сила действует на тело в»направлении» параметра J, равного K (g) на единицу объема, получается из вариационного условия (минимальная свободная энергия): 6t-Jx ® 6E ® dV = eJSFK, l] dV-Jx ® 6 ® = 0£ Л [Дж]—0 *(р).
Если p (r, r *) является зеленой функцией оператора (ξ), то функция {®=■ » J p (r, r ’) J ® dV ’ является решением уравнения в правой части C. Для граничных условий)¥ [£] −0. (упомянутый ранее в букве r (29.10)), указывая расстояние от dV до точки наблюдения, обнаруженной A £х-а j-де-ехр (р + с)} дв、 Где A = » Lo-расстояние от некоторой средней точки 0. Расстояние в. Если расстояние A очень велико, то его можно разложить по строкам до координат элемента dV, который определяется радиус-вектором r.
Для пространственно однородного элемента упругой среды при его продольной деформации примером термического уравнения состояния служит закон Гука. Людмила Фирмаль
Л-Л-(Д » Г)、 Де = — ^-5 (Р). I1 = ALE15′) ’_ и, ’G, L,’ 339) Здесь вектор s = k0-k, где k0 — волновой вектор падения, k-рассеянный свет, поэтому| k,| = / k0 | — 2l /)., А r обозначает радиус-вектор E, отсчитываемый от начальной точки объема V. интенсивность рассеянного света пропорциональна квадратному коэффициенту этого amount. In другие слова、 «=■Ф 5 (р)й (р ’)ЕІ, — r_r’)з ’= =(f P(r, r.) e’I, — l-r ’ dVdV’.(33.10) Таким образом, интенсивность падающего света как единое целое, для рассеянной интенсивности света、 Значение Интеграла легко найти.
Во-первых, заметим, что для однородных и изотропных объектов функция p (r, r ’)зависит только от расстояния| r-r’ |между точками r’, так что p = p (|r-r’|).Заполните форму (33.9) в выбранном месте я = г п (/г-р’!) Сумма p «n, ’r_r’)1r ’ = C, очевидно, не зависит от V. Тогда при запуске интеграции на dV、 И-CSS, и С =] р(| р-р’|)»».’—’»¿год.—». «И (г)、 (33.11) Однако, поскольку p (|m-r ’|) является функцией Грина(для бесконечной области) иsup class=»reg»>®/sup>является решением уравнения Но 33.11.
Смотрите также:

