Оглавление:









Выбор оптимального портфеля ценных бумаг агентом, не склонным к риску
- Выбор оптимального портфеля ценных бумаг агентами, не склонными к риску Обеспечение наличия множества различных финансовых активов облегчает инвесторам выбор их на фондовом рынке по всему миру. В этом разделе мы рассмотрим теоретические основы выбора портфеля ценных бумаг из всех активов, доступных для инвесторов.
- При каких условиях инвесторам требуются разные виды активов? Какова взаимосвязь между спросом на конкретные финансовые активы и связанными с этим рисками и ожидаемой доходностью? Современные теории выбора портфеля предоставляют несколько подходов к решению этих важных проблем.
Во-первых, большинство инвесторов не защищены от риска, то есть они не только максимизируют ожидаемую доходность, но и снижают риск. Людмила Фирмаль
Считается, что агент нейтрален к риску, если агент сосредоточен только на ожидаемой норме доходности портфеля и не обеспокоен риском. Однако, если большинство агентов на самом деле нейтрально к риску, люди не покупают страховку, а инвесторы не пытаются диверсифицировать свой финансовый портфель. Им нужен только один актив.
Это обещает самый высокий ожидаемый доход. Тем не менее, представляется разумным предположить, что инвесторы не склонны к риску, поскольку агенты покупают страховки и прилагают большие усилия для диверсификации своих портфелей. Если агент не избежит риска, он попытается распределить богатство среди множества доступных активов9. главная 9 См.
Главу 4 для более глубокого юридического анализа этого вопроса. Книги 6 и 7: Уильям Шарп и Гордон Александр. Инвестиции (Englewood Cliffs. Н.Дж.: Прентис Холл. 1990). Концепция портфельной теории агента по избежанию риска — «Не кладите все яйца в одну корзину». В мире международных финансов действуют следующие правила: «Не вкладывайте все свое богатство в финансовые активы одной страны или в одну валюту».
Формально портфель — это набор активов, как финансовых (деньги, облигации, акции и т. Д.), Так и реальных (земля, золото, картины и т. Д.). Теория портфеля начинается с утверждения, что владельцы активов должны обращать внимание на характеристики всего портфеля, а не обращать внимание на некоторые отдельные компоненты или активы.
Активы, которые подвергаются риску сами по себе, полностью надежны в портфеле, который включает другие активы, которые компенсируют этот риск. Поэтому инвесторы предполагают, что они заинтересованы в двух ключевых показателях рискованного портфеля: ожидаемой доходности и риске, отраженном в диверсификации портфеля.
Основа теории выбора портфеля была впервые разработана в статье, опубликованной в начале 1950-х годов лауреатом Нобелевской премии Гарри Марковицем10. Наиболее важным моментом является то, что агенты пытаются достичь оптимального сочетания риска и доходности портфеля.
По этой причине оптимальной инвестиционной стратегией является владение портфелем, который сочетает в себе диверсификацию портфеля, то есть широкий спектр небольших сумм различных финансовых активов. Чтобы определить оптимальное поведение при формировании портфеля, вам необходимо понять, как его риск и доходность зависят от риска и доходности актива.
После того как вы установили связь между инвестиционным портфелем и характеристиками всех его активов, вы можете найти оптимальную структуру. Ожидаемая доходность портфеля Чтобы определить ожидаемую доходность портфеля активов, начните с концепции ожидаемой доходности отдельных активов.
Предположим, что доходность долгосрочной облигации компании Maxum составляет 10% с вероятностью 50% и 20% с вероятностью 50%. Ожидаемая норма доходности — это средневзвешенное значение возможных ставок доходности, а вес — соответствующая норма доходности .В этом примере ожидаемая доходность составляет 15%: 0,5 (10%) + 0,5 (20%).
В общем случае, если доходность актива равна g, есть ли вероятность возврата g? -Возможность р2у доходности / 3-Вероятность ру и т. Д. До рН-Если есть вероятность, ожидаемая норма доходности актива равна: r — />, r, + r2r2 + /> 3r3 + … + Rn „(20,1) Вероятность уравнения (20.1) должна быть равна единице: p] + p2 + Сделайте инвестора владельцем портфеля с N различными активами. Предположим, что инвестор имеет определенное богатство WQ и инвестирует в n активов.
Доля портфеля, инвестированного в актив y, выражается в aJ%. В общей сложности активы инвестируются в; W0. Доля всех активов должна быть 1, поэтому i, + a2 + a3 + … + an = 1. 10 «Выберите портфолио». Журнал финансов. Март 1952 г. Теперь рассчитайте ожидаемый доход для всего портфеля. Это показано как g *. Сначала определите ожидаемый доход для каждого из N активов, используя формулу, которую вы только что приобрели.
Они обозначены как rf, rj, r \ для активов 1, 2 и n соответственно. Далее, ожидаемая норма доходности для портфеля (гр) рассчитывается как средневзвешенная доходность n активов в портфеле, где вес — это доля портфеля, вложенного в каждый актив. Формат: gr «a \ rf + a2r2 + — + aL • (20.2) Следовательно, ожидаемая доходность портфеля зависит как от нормы доходности каждого актива в портфеле, так и от активов, вложенных в эти активы.
Давайте рассмотрим простой пример. Предположим, у вас есть два актива, 1 и 2. Ожидаемая норма доходности для актива 1 составляет 10%, а норма доходности для актива 2 составляет 20%. Если портфель равномерно распределен между этими двумя активами, т.е. Если = a = 0,5, ожидаемая доходность портфеля составляет 15%: 0,5 (10%) + 0,5 (20%).
Если 75% средств инвестируются в Актив 1 и 25% в Актив 2, ожидаемая доходность составляет 12,5%: 0,75 (10%) + 0,25 (20%). Инвестор примет решение на основе ожидаемой доходности портфеля (гр., А фактический результат вложения средств будет зависеть от фактической доходности.
I’oO + Очевидно, что размер WQ равен размеру Wx Зависит только от фактической доходности гр, но инвесторы не знают значение гр, поэтому они должны принимать решения на основе информации, которую они имеют: ожидаемая норма прибыли (гр и риск, это Перейти к Портфельный риск Портфельный риск может быть измерен по дисперсии доходности, которую он приносит.
Сначала рассмотрим концепцию индивидуальной диверсификации активов. Инвесторы сталкиваются с двумя разными активами: акциями Prudence Bank, доходность которых всегда составляет 8%, и акциями Jambl, которые не приносят доход в плохие годы (доходность 0%), но приносят огромную прибыль Удачный год (доходность 16%). Ожидаемая доходность обеих акций составляет 8%.
Однако разумные акции не подвержены риску, а запасы варенья опасны в том смысле, что доходность колеблется. Обычно используемой статистической мерой риска является дисперсия A1. Формально распределение доходов от активов определяется как сумма квадратов отклонений от среднего дохода.
Каждое отклонение имеет вес, равный вероятности получения именно этого дохода. Используя приведенные выше обозначения, предположим, что доходность актива равна r, r2, …, rn, а вероятности равны pv p2, …, rn соответственно. Ожидаемая доходность рассчитывается по уравнению (20.1), а дисперсия определяется следующим образом: -PiCi-O2 + P2C2-g ‘) 2 + — + Pn (r „-rf) \ (20,3)
В примере с двумя банками ожидаемая доходность для обоих составляет 8%, но разница отличается. Для разумных банков диверсификация 0% (8–8%), что означает отсутствие риска для этого актива. Для банка Jamble, распределение: A2-0,5 (0,0-0,08) 2 + 0,5 (0,16-0,08) 2 = 0,64 Стандартное отклонение a — еще одна мера традиционного риска в портфельном анализе — равно квадратному корню из дисперсии.
Ноль для первого актива и 0,8 для второго актива. Следующим шагом является вычисление дисперсии портфеля (a2) на основе дисперсии активов в портфеле. Диверсификация портфеля — это не простая средневзвешенная диверсификация активов (как в случае ожидаемой доходности). Чтобы понять, почему это так, давайте рассмотрим пример.
Предположим, что инвестор владеет акциями двух компаний, и половина каждого актива инвестируется. Raincats Limited, одна из компаний, проектирует и продает дождевики. Если год очень дождливый и происходит в половине случаев, рентабельность акций компании составляет 25%. Если год солнечный (вторая половина), доходность составляет всего 5%.
Вторая компания (производитель солнцезащитных очков), Sanglagiz Limited, дает 25% дохода в солнечные годы и только 5% в случае необычно дождливых лет. Ожидаемая норма прибыли для обеих компаний составляет 15% в год, а разница для обеих компаний составляет 0,01. «Это означает, что отклонение портфеля инвесторов также составляет 1% (средневзвешенное значение двух соответствующих отклонений)?
Очевидно, ответ — нет. В сезон дождей инвесторы получают 25% дохода от акций Rinkots Limited и 5% от акций Sanglasez Limited. Портфель возвращает 15% (0,5 (25%) + +0,5 (5%)], поскольку половина актива инвестируется в половину актива, а также из 25% акций Sanglagiz Limited. Доходность портфеля снова составляет 15%, напомним этот самый важный результат.
Инвесторы могут получить портфель с нулевым разнообразием. Безрисковое портфолио! В этом случае говорят, что доходность имеет отрицательную корреляцию, потому что один актив имеет тенденцию расти выше среднего уровня, а другой актив ниже среднего уровня. Другими словами, есть отрицательная ковариация в возврате, мы определим это понятие более точно и немедленно.
- Наш инвестор делит акции Rainkotes Limited в сочетании с акциями компании-производителя зонта Umbrellas Limited, которые получают хорошую прибыль в дождливый год (доходность 25%) и плохую в солнечный год (доходность 5%). Давай купим Поэтому производители дождевиков и зонтиков имеют одинаковую структуру прибыли.
Если инвестор владеет половиной активов каждой компании, ожидаемая доходность портфеля составляет 15%, но риск выше, потому что риски обоих активов не компенсируют друг друга. Диверсификация портфеля, состоящего из «Ожидаемая доходность для каждого актива составляет 15% (0, S (2 $%) + 0, S (S%)).
Разница составляет 0,01–0,5 (0,25–0,15) + 0,5 (0,05–0,15) *. 0,01 из этих двух активов соответствует дисперсии отдельных активов12. Людмила Фирмаль
В этом случае возврат двух активов, как говорят, имеет положительную корреляцию, то есть положительную ковариацию. Теперь вы можете официально представить концепцию ковариации между двумя активами. Используйте это определение для расчета дисперсии всего портфеля как функции дисперсии активов и ковариации. Рассмотрим два актива, один и два.
Каждый актив имеет определенную выгоду, связанную с риском. Предположим, что доходности r и r2p этих активов с вероятностью p равны -роль r, 2 и r22 и т. Д. С вероятностью p2. Предположим, что существует n возможных комбинаций результатов и n вероятностей, соответствующих этим результатам. Ожидаемая норма доходности для актива рассчитывается обычным способом, обозначенным r \ и r \ соответственно.
Ковариация доходностей двух активов показана как cov (rp g2) и рассчитывается следующим образом: COV (r ,, r2) -P [(GI-Ge [) (G21-Ge2) + MG12-G ‘) (G22-G2) + / <1L l (ZU.4) + + Pn (Gxn-T1) (T2, r2) — Ковариантность положительна, если доходность активов в то же время выше среднего. Если доходность активов не зависит друг от друга, ковариация равна нулю. Если доходность одного актива выше среднего, а доходность другого актива ниже, ковариация отрицательна.
Это показывает, как общая диверсификация портфеля зависит от характеристик риска каждого актива в портфеле. Принимая во внимание портфель, который первоначально состоит только из двух активов, дисперсию портфеля можно рассчитать с использованием приведенного ниже уравнения 3. st2 _ -2.-2. -2_2 a \ Oy + a {o2 + 2 <7, a2cov (r ,, r2). (20.5)
Что говорит мне это выражение? Диверсификация портфеля — это взвешенная сумма диверсификации активов в портфеле, и первый член зависит от ковариации активов. Если ковариация отрицательна, этот термин уменьшает общую дисперсию портфеля. Риск таких активов в принципе компенсирует друг друга.
Потому что рентабельность 1 12 Формула для распределения дохода для портфеля, включающего два актива (I и 2), выглядит следующим образом: vat (rf) -var (in, r, + in /,), используя определение r, w в формуле (20.2) van g,) — djvar (r,) ”ajvardy ♦ 2l, o; sow (l, g;), de cov (r, «a (I a pl2- поправка между возвратом активов I и 2; 1 Дисперсия пор может быть измерена. Лист hcxo.w из определения дисперсии уже применяется.
Если есть возможное значение v для прибыльности:> (в зависимости от вероятности превышения активов в портфеле), укажите вероятность получения разных доходов через строку «/>. Определите ожидаемую доходность портфеля, а затем отклонение портфеля определяется следующим образом: o2-LO. GR: g «U ** <20.5a) ♦ • ■■ ♦ ‘.a. P Высокая и еще одна низкая доходность.
Если ковариация положительна, последний член увеличивает дисперсию всего портфеля. Вы также можете дать более общее выражение (без доказательства) дисперсии портфеля активов: a) -a} a2y + a \ o \ + … + a \ a \ + + 2a {a2cov (rrr2) + 2alaicoy / (rvri) + … + 2alancov (rltrn) + (ZU.O) + 2a2ab cov (r2, r3) + 2J2fl4cx) v (r2, r4) + … + 2d2d „sow (r2, rj) + + ••• + 2Vifl «cov (Vi’r») — Ожидаемая полезность как функция риска и доходности.
Основная проблема для владельцев активов заключается в том, как распределить по n активам таким образом, чтобы максимизировать ожидаемую полезность, то есть как выбрать часть портфеля. Теория портфеля предполагает, что владельцы активов стремятся максимизировать ожидаемую полезность (Ue).
Это зависит от ожидаемой доходности портфеля (g *) и риска, измеренного операцией стандартного отклонения (напомним, что стандартное отклонение портфеля возведено в квадрат) — корнем его отклонения). Таким образом, вы можете написать: U ‘-U’ (r’p, ap). (20L)
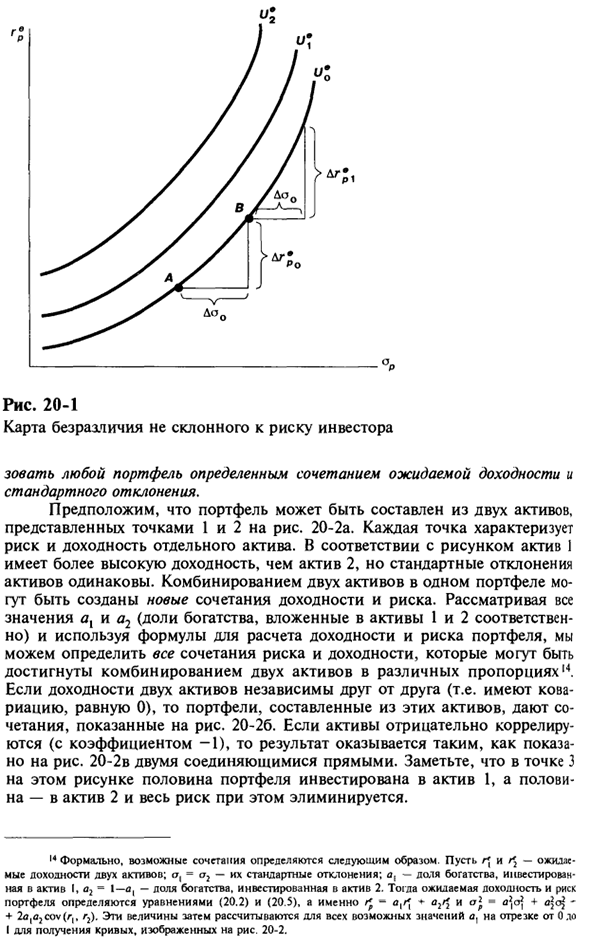
Уравнение (20.7) Полезность, ожидаемая инвесторами, увеличивается с увеличением ожидаемой доходности портфеля и уменьшается по мере того, как доходность становится более волатильной. Когда ар увеличивается. Вы можете создать карту кривых безразличия, которые связывают доходность и стандартное отклонение (Рисунок 20-1).
Беспорядочная кривая обычно соединяет все точки, которые соответствуют уровню счастья или полезности. В этом случае разнородная кривая соединяет все точки ожидаемой полезности на одном уровне. Риск, выраженный в стандартном отклонении, уменьшает полезность, и чем выше ожидаемая доходность, тем выше полезность, поэтому кривая безразличия имеет положительный наклон.
Перемещаясь из пункта А в пункт В, инвесторы остаются на том же уровне выгод, что компенсирует более высокие риски и более высокие ожидаемые доходы. Уровень полезности увеличивается с увеличением ожидаемого дохода, когда риск постоянен, или с уменьшением риска, когда ожидаемый доход постоянен.
Поэтому на рисунке 20-1 приведенная выше кривая безразличия связана с более высоким уровнем полезности. Состав портфолио Предпочтения инвестора — это только одна сторона вопроса выбора портфеля. Другая сторона — доступный выбор. В принципе, инвестор может выбрать из всех существующих активов и построить возможный портфель из любого количества акций, представляющих эти активы.
Таким образом, каждый актив или каждая комбинация активов в портфеле могут быть представлены одной точкой с координатой «риск-доходность». Это можно охарактеризовать Рисунок 20-1 Безразличная карточка безразличия для инвесторов Назовите портфель с определенной комбинацией ожидаемой нормы прибыли и стандартного отклонения.
Предположим, что портфель может состоять из двух активов, представленных точками 1 и 2 на рисунке 1. 20-2a. Каждая точка характеризует риск и доходность отдельного актива. Согласно рисунку, актив 1 имеет более высокую доходность, чем актив 2, но стандартное отклонение активов такое же.
Комбинируя два актива в одном портфеле, вы можете создать новую комбинацию доходности и риска. может быть достигнуто путем рассмотрения всех значений ay и a2 (доли активов, инвестированных в активы 1 и 2 соответственно) и объединения двух активов в различных соотношениях с использованием формул доходности портфеля и риска Все комбинации риска и доходности могут быть определены14.
Если доходность двух активов не зависит друг от друга (то есть ковариация равна 0), портфель, состоящий из этих активов, дает комбинацию, показанную на рисунке. 20-26. Если актив имеет отрицательную корреляцию (с коэффициентом -1), результат показан на рисунке. 20-2 с двумя соединительными прямыми.
Обратите внимание, что в точке 3 на этом рисунке половина портфеля инвестируется в актив 1, а половина инвестируется в актив 2, что исключает все риски. 14 Формально возможные комбинации определяются следующими режущими кромками. Пусть r \ u будет ожидаемой доходностью двух активов. Art = A2-стандартное отклонение. а доля активов, вложенных в актив I. а2 ~ 1 — о доля активов, вложенных в Актив 2.
Ожидаемая доходность и риск портфеля затем определяются уравнениями (20.2) и (20.5). ♦ arf и o * -a ^ o * + — + 2 <j, flJcov (rl, r2). Эти значения рассчитываются для всех возможных значений o с интервалами от 0 до I, чтобы получить кривую, показанную на рисунке. 20-2. (А) G9 < (В) Рисунок 20-2 Возможный состав портфеля из двух активов.
Различные наборы портфелей, которые могут быть сформированы из комбинации Актива 1 и Актива 2, имеют сложные имена или приемлемые наборы портфелей. Комбинируйте все комбинации рисков и доходов, которые вы получаете при выборе разных портфелей.
Конечно, на практике инвесторы стремятся сосредоточиться на некотором важном подмножестве набора приемлемых портфелей, а именно на наборе эффективных портфелей. Каждому из двух случаев, показанных на рисунке, соответствует 20-2, а верхняя часть кривой портфеля отмечена жирной линией.
Оба представляют эффективные и приемлемые портфели в том смысле, что они либо дают наибольшую доходность при определенном риске, либо наименьший риск при определенной доходности. Инвесторы постоянно стремятся создать эффективный портфель для максимизации ожидаемой доходности.
Например, из рисунка 20-2c, портфель C (включая 75% актива 1 и 25% актива 2) также доступен, поэтому инвестор может выбрать портфель B (25% актива 1 и актива 2) Не выбирайте (в том числе 75% из 2). Портфель C имеет такой же риск, но более прибыльный, чем портфель B. В отличие от портфеля B, портфель
C является эффективным портфелем (потому что нет способа заработать высокую прибыль без увеличения риска). к (В)Рисунок 20-26 находится на кривой, соединяющей точки A и 1, а на рисунке это 20-2B- на линии, соединяющей точки 1 и 3. Выберите лучшее портфолио Мудрый инвестор, очевидно, выберет портфель из множества эффективных портфелей, какой выбрать?
Чтобы найти лучший из всех действительных портфелей, вам нужно вернуться к случайной кривой на диаграмме. 20-1. Рассмотрим случай, когда два актива независимы, как показано на рисунке. 20-26. На рисунке он увеличен и воспроизведен. 20-3 и неизбирательные кривые. Как всегда, инвесторы стремятся выбрать портфель, который может достичь лучшей кривой безразличия.
Также ясно, что его выбор ограничен многими эффективными портфелями. Равновесие портфеля достигается на пересечении многих эффективных портфелей (кривая от А до 1) и лучшей кривой безразличия. Разнородная кривая фигуры U \ достигает равновесия 20-3 в точке £, касающейся действительного множества. Обратите внимание, что точка E соответствует обоим портфелям активов.
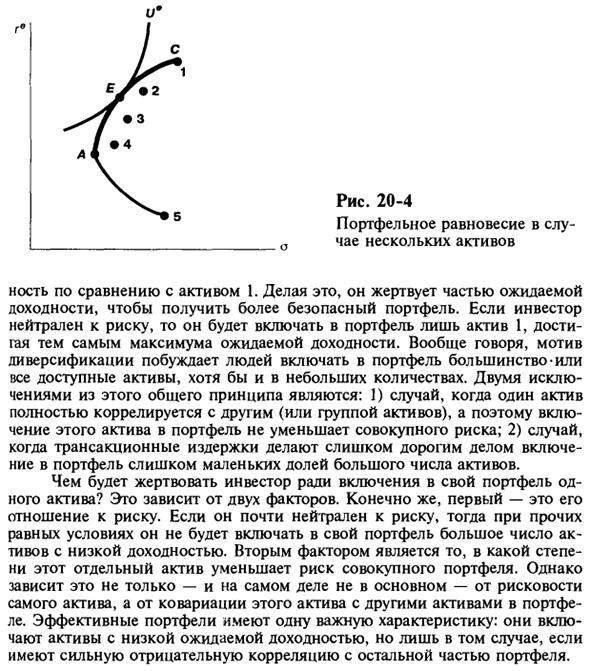
Это имеет место в общих случаях. Конечно, инвесторы хотят достичь уровня полезности £ / $, но это невозможно, потому что нет портфеля с такой выгодной комбинацией риска и доходности. Вы можете использовать алгебраические преобразования, чтобы распространить этот анализ на случаи с несколькими активами. На рисунке 20-4 показаны пять активов, обозначенных точками 1-5.
Комбинируя эти точки, вы можете найти набор доступных портфелей, обозначенных областью, окруженной кривой C-5. Равновесие портфеля снова достигается в точке «. Здесь кривая безразличия связывается с действительным набором портфелей. В общем, точка E соответствует портфелю, содержащему пять или все существующие активы. вы.
Некоторые характеристики оптимального портфеля Вернемся к равновесию фигуры. 20-3. Инвесторы, ищущие оптимизации, включают актив 2 в портфель, но доходность этого актива низкая 1 но Рисунок 20-3 Эффективный набор, эффективный набор, баланс портфеля Делая это, по сравнению с Активом 1, жертвует частью ожидаемой доходности, чтобы получить более безопасный портфель.
Если инвестор нейтрален к риску, достигните максимальной ожидаемой доходности, включив в портфель только актив 1. Вообще говоря, мотивы диверсификации способствуют включению большинства или всех доступных активов в портфель, даже в небольших количествах.
Два исключения из этого общего принципа: 1) Поскольку один актив полностью коррелирует с другим активом (или группой активов), включение этого актива в портфель не снижает общий риск. 2) Стоимость сделки слишком высока для включения в портфель и, следовательно, содержит слишком мало акций большого количества активов.
Чему жертвует инвестор, чтобы включить один актив в портфель? Это зависит от двух факторов. Конечно, во-первых, его отношение к риску. Если он практически нейтрален к риску, он не будет включать в портфель большое количество активов с низкой доходностью. Второй фактор — насколько этот отдельный актив снижает общий риск портфеля.
Однако это зависит не только от риска самого актива, но на практике это также в основном зависит от ковариации этого актива с другими активами в портфеле. Эффективный портфель имеет одну важную особенность. Включает активы с низкой ожидаемой доходностью, но только в случае сильной отрицательной корреляции с остальной частью портфеля. о Рисунок 20-4 Баланс портфеля нескольких активов
Смотрите также:
Если вам потребуется заказать решение по экономической теории вы всегда можете написать мне в whatsapp.

