Введение в кинематику. Способы задания движения точки

Введение в кинематику. Способы задания движения точки

• Введение в кинематику. Как придать частице подвижность мо механизм изучает движение тела или материальной точки, независимо от причины этого движения, а также физические свойства тела и физические или физические характеристики в это время. Движение понимается как изменение положения тела или материальной точки в пространстве с течением времени. Это положение определяется в любой системе координат, строго

связанной с несколькими телами. Эта система называется системой отсчета. Тело, в котором рассматривается упражнение, называется эталонным телом. Обычно количество тел занимает Земля. В кинематике предполагается, что скорость движения тела намного меньше скорости света, поэтому положение тела в пространстве относительно выбранной системы отсчета определяется пользователем.

Положение объекта в пространстве изменяется со временем, время не зависит от выбранной системы отсчета. Все Людмила Фирмаль

остальные переменные (расстояние, скорость, ускорение) являются функциями времени. Единицы измерения времени Си-секунды, а единицы измерения длины-метры (м). Время отсчитывается от некоторой заранее выбранной начальной точки (/=0). Временной интервал Az= / 2-определяется числом единиц времени, прошедших от более раннего времени T\до более позднего t2. Воображаемая непрерывная линия, описываемая точкой движущегося тела

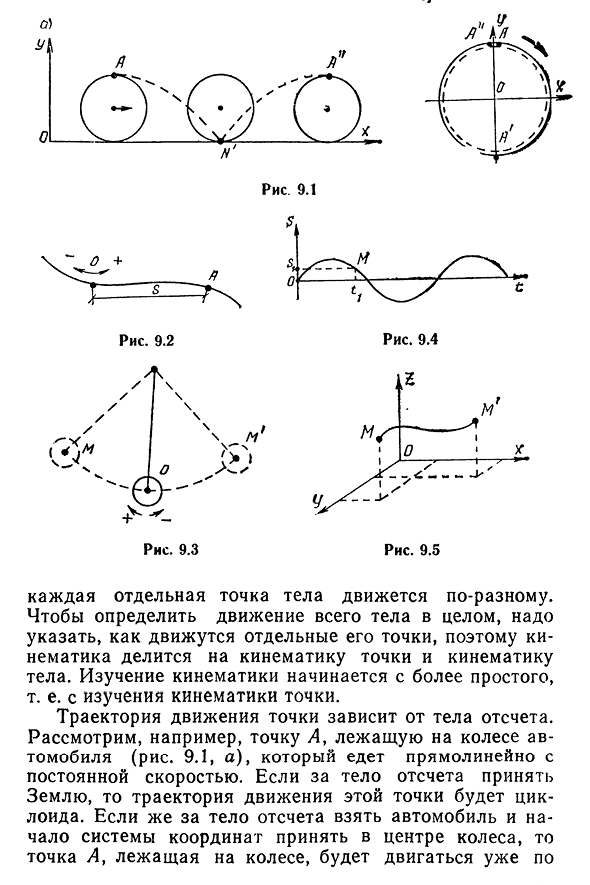
относительно заданной системы отсчета, называется траекторией движения. Траектория движения является криволинейной и линейной. В линейном движении все точки тела движутся одинаково. В криволинейном движении 78Б) Рис Рис. 9. 3. 9.5 Каждая отдельная точка тела движется по-разному. Чтобы определить движение всего тела, необходимо указать, как движется каждая отдельная точка, поэтому кинематика делится на точечную кинематику и соматомотонику,а изучение кинематики начинается с более простой. Траектория точки зависит от тела отсчета.

• Рассмотрим, например, точку L, которая находится на колесах автомобиля(рис. 9.1, а) движется линейно с постоянной скоростью. Принимая землю за опорное тело, орбита этой точки становится циклоидой. Если тело отсчета берет начало координат системы, чтобы взять в центре колеса с автомобилем, точка L будет лежать на колесе и двигаться дальше уже 79 иен(рис. 9.1, 6). Движение кривой точки можно определить двумя способами: естественным и координатным. Давайте сначала рассмотрим естественный путь. Этот метод удобен, если известна траектория движения точки а(рис. 9.2). Затем выберите точку отсчета O, в которой начало координат

находится на этой орбите. В этом случае траектория является криволинейной осью. Положение точки А в заданное время определяется законом движения по заданной траектории: s=f (O. (9.1) Здесь координата кривой s представляет собой длину отрезка от опорной точки O до временного интервала t до точки A. Функция f (t), точка движения в любой момент времени может присутствовать только в одном месте, при ее движении по заданной траектории вычисляются все положения на кривой. Итак, чтобы задать движение точек естественным образом, нужно указать: 1) локус точек;2) положительное направление опорной точки и опорную точку на этой траектории.

Следует отметить, что закон движения (9.1) определяет Людмила Фирмаль

не траекторию движения, а положение материальной точки на ее орбите. Например, когда маятник вибрирует в локусе точки М(рис. 9.3) становится дугой мм’. Если опорная точка O принимает положение статического равновесия, то координата кривизны s абсолютной величины всегда будет меньше или равна длине дуги-ом, а путь всегда положителен, и поэтому все точки равны. То есть он проходит O, M, M ‘ в ряду и снова становится точкой O. Описание закона движения в 80 точках обычно отражает зависимость координаты s от графика движения, то есть зависимость координаты s от времени t, и рассмотрим движение центроида маятника во время

колебаний на примере использования кривой, характеризующей движение точки вдоль оси вращения. В этом случае график движения является синусоидальной волной. 9.4). На этом графике, прежде всего, можно легко определить смещение точек во времени. Таким образом, во времени/1 криволинейные координаты SJ. Во-вторых, по построенному графику можно определить пройденное расстояние. Например, во времени L (см. диаграмму. 9.4) пройденное расстояние будет равно длине дуги ом. График движения не следует путать с локусом движения. Таким образом, в приведенном выше примере график движения представляет собой синусоидальную волну (рис. 9.4), траектория движения-дуга мм'(см. 9.3). В координатном методе,

задающем закон движения точки, необходимо знать положение точки между каждым моментом времени, то есть задавать координаты точки как функцию времени t. Чтобы указать местоположение точки, используйте систему координат, которая удобна для данного конкретного случая. Следовательно, x, y, z (рис. 9.5) закон движения точки задается в виде уравнения движения точки: х=х(т), г=г(Ф), з=з(Т). (9.2) Понятно, что уравнение в параметрической форме (9.2) определяет траекторию движения. Если исключить параметр t из (9.2), то можно получить траекторию самого движения. Если точка движется по плоскости, то одна координата g

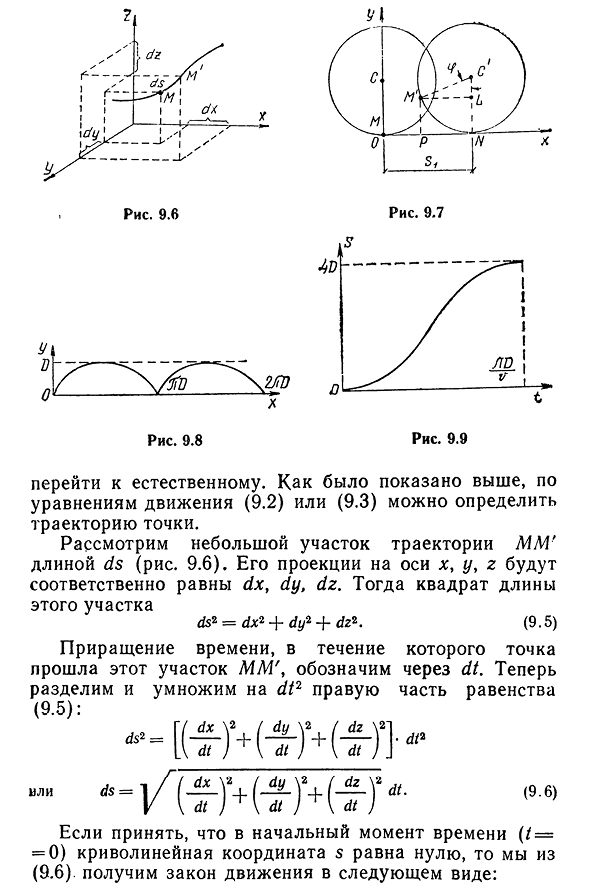
равна нулю,и получается только два уравнения движения: x=x ( / ), y=y(t). (9.3) Например, при прямолинейном движении точки вдоль оси x, в этом случае мы получаем только уравнение движения, которое естественным образом совпадает с законами движения, определяющими движение точки: x=x(0. (9.4) Из метода координат, определяющего перемещение 6-480 81.1 9.6 Рис 9.8 Иди на природу. Как указано выше, можно определить траекторию движения определенной точки с помощью уравнения движения (9.2) или (9.3). Рассмотрим небольшой участок трассы мм ‘ длиной ds(рис. 9.6). Проекция на оси X, y и z будет равна dx, dy и dz соответственно. Тогда квадрат длины этого участка ds=dx+DY*+dzK (9.5) Приращение времени прохождения точки через этот участок мм ‘ указывает на dt.

Затем разделите правую часть уравнения на dt2 и умножьте его Или (9.6) Если предположить, что координата кривой s равна нулю в первый раз(/==0), то это из(9.6). Мы получаем законы движения в виде: 82(9.7. Когда точка движется по плоскости, равенство (9.7) принимает вид: Например. Найти уравнения и законы движения, построить график движения точки М(рис. 9.7), расположенный на краю колеса, которое катится равномерно, не скользя по прямой линии. Диаметр колеса равен D, закон движения оси колеса задается в виде решения, а ось x принимает прямую линию, по которой вращается колесо. Начало координат берут в точке М на ободе колеса впервые. В какой-то момент времени t ось колеса будет находиться в положении C ‘ (см. рис. 9.7). Длина дуги в NM ‘ равна расстоянию N O=v0t, так как колесо катится без скольжения.: Q. Наконец, мы получаем закон движения точки M в виде: s=2D^1-c o s — ^ — j. Он показывает график движения точки M на рисунке. 9.9

Смотрите также:

Решение задач по технической механике

Расчет на прочность и жесткость при кручении	Скорость точки
Изменение моментов инерции при параллельном переносе осей	Ускорение точки

Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.