Оглавление:
Второй замечательный предел
Как известно, предел числовой последовательности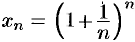 
, 
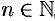, имеет предел, равный 
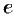(см. (15.6)):
Докажем, что к числу 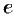стремится и функция 
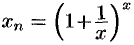при 
:
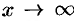
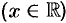1. Пусть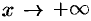 
. Каждое значение 
заключено между двумя положительными целыми числами: 
, где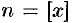 
— это целая часть . Отсюда следует 
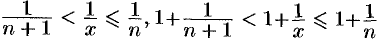, поэтому
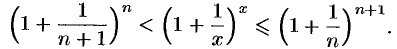
Если 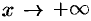, то 
. Поэтому, согласно (17.14), имеем:
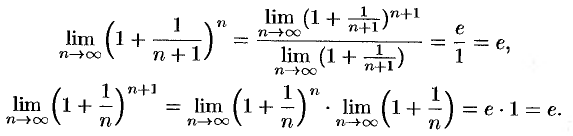
По признаку (о пределе промежуточной функции) существования пределов
Пусть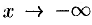 
. Сделаем подстановку 
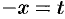, тогда
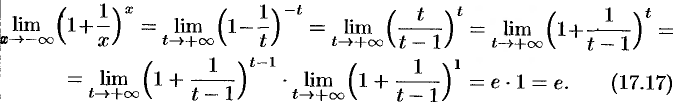
Из равенств (17.16) и (17.17) вытекает равенство (17.15).
Если в равенстве (17.15) положить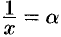 
(
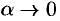при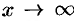
), оно
запишется в виде
Равенства (17.15) и (17.18) называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием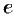
. Функция 
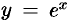называется экспоненциальной, употребляется также обозначение 
.
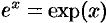Пример №17.8.
Найти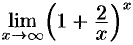 
.
Решение:
Обозначим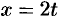 
, очевидно, 
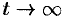при 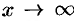. Имеем
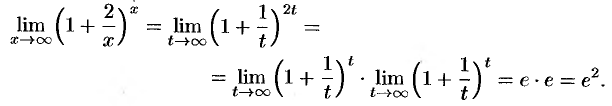
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Основные элементарные функции |
| Первый замечательный предел |
| Эквивалентные бесконечно малые функции |
| Производные основных элементарных функций |
