Оглавление:




Вращающийся диск постоянной толщины
- Вращающиеся диски постоянной толщины. Фигура. Пятьсот восемьдесят шесть Улучшение проблемы напряжений и растяжений происходит за счет высокой скорости вращения вала и диска. Высокая скорость вращения вала паровой турбины, вала и диска вызывает появление критической центробежной силы. Вызванные ими
напряжения распределяются симметрично относительно оси вращения диска. Рассмотрим простейшую задачу расчета диска определенной толщины. Расчет такого диска является приближенным решением метода расчета диска. Воспользуемся некоторыми результатами, полученными при выводе формулы для расчета толстых цилиндров (§ 197).
Предположим, что толщина диска равна одному напряжению иЛюдмила Фирмаль
считается равным нулю. Приведем условие равновесия элемента AB, отделенного от диска двумя меридиональными сечениями и двумя концентрическими цилиндрическими плоскостями(рис. 586). Сила, действующая на плоскость элемента AB, сила инерции также должна учитываться В этом случае krome682 учитывает силы инерции и вибрации[CH. XXXV От центра по радиусу до внешнего контура
диска. Вместо формулы (32.1), выведенной из§ 197, мы имеем: (35.4) Уравнение того же пункта (32.4) (условие деформационной подгонки) остается справедливым для этой задачи. (35.5) Подставляя значение разности в это выражение<ZG-z, из(35.4) находим: (35.6) Дифференцируя уравнение (35.4) на G и подставляя его значение из уравнения (35.6), получаем линейное дифференциальное уравнение Или dr r d r x r / интегрирование этого уравнения、:
- — r2g=0. (35.7) Это из(35.4) и (35.7) (35.8) В формулах (35.7) и (35.8) A и B являются постоянными интегралами, которые должны определяться из условий контура диска. 1) диск с отверстием в центре и 2) сплошной диск. В этом случае сначала предположим, что на краю диска нет внешней силы. Для дисков с центральным отверстием напряжение AG должно быть равно нулю как для G=GP, так и для G = G2(рис. 586). Эти условия на контуре при подстановке их в уравнение (35.7) приводят к уравнению: Откуда — R2G? О= , Подставляя
значения A и B в выражения (35.7) и (35.8: И ° / =p3 4-p. —-(1+G2j — § 219]вращающийся диск постоянной толщины 683 Предположим, чтобы быть кратким 1+3Р.3+ПТ =ч Мы пишем: И (35.9)) (35.10) Заметим, что напряжение AG равно нулю при p=1, а p=a, то есть внутреннее напряжение AG имеет одинаковую величину
И внешний контур диска. Около Значение p между 1 и a достигнет самого Людмила Фирмаль
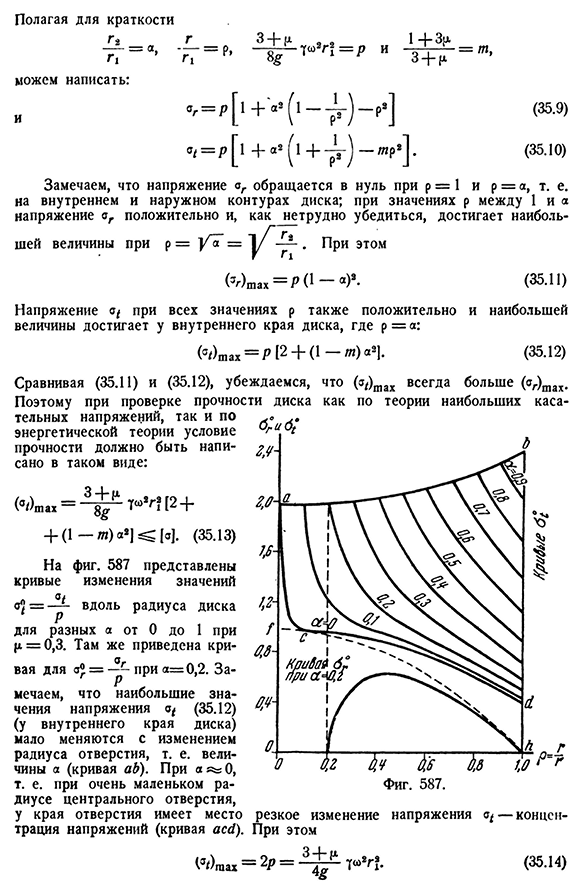
высокого значения- Этот (Jr) m A x=P0 -°) 8-напряжение a/при всех значениях P (35.11) также является положительным и достигает максимального значения на внутренней кромке диска.[2 + ( 1 — / » ) » 21. Сравните (35.12) (35.11) и(35.12), и убедитесь, что (a-z) m ax всегда больше, чем (ZG) t A x. Итак, если проверить прочность диска как по теории максимального касательного напряжения, так и по теории энергии, то условие прочности следует записать в таком виде.: Как использовать кривую изменения величины 587 = 0 на 1p вдоль радиуса диска, = 0,3 указывается для разных a. есть также кривая
с A®=~a=0,2. Отметим, что при изменении радиуса отверстия, а именно величины a (кривая ab), максимальное значение напряжения (35.12) (внутренняя кромка диска) практически не изменяется. A » s0, то есть с очень малым радиусом отверстия в середине, есть коррекция напряжения в конце отверстия (кривая acd). В то же время (а<)тах=2Р — В личку Фигура. Пятьсот восемьдесят семь Внезапное изменение напряжения концентра- (35.14) 684 с учетом силы инерции и силы вибрации[Глава II. XXXV (35.15)) Напряжение и ток- Для очень жидких колец, at и A^1, /- И _ \ / / G максимальное » Это совпадает с заключением§ 217. В этом случае максимум (35.15) составляет чуть более 20% (Вт/) t A x для дисков
с очень высоким профилем (20.14). Из формул(35.9) и (35.10) видно, что он растет очень быстро с увеличением напряжения<ЗГ и окружной скорости диска^=<0^. Заметим, что помимо свойств скорости v и материала p и y, эти напряжения зависят только от безразмерных величин p и A. Это обстоятельство позволяет заменить заводские испытания дисков большого диаметра лабораторными испытаниями модели. Для твердого диска центр диска, то есть напряжение и напряжение g=0, должны быть равны друг другу. Если мы сравним выражения (35.7) и (35.8), то мы уверены, что константа B должна
быть y, чтобы удовлетворить этому условию. Постоянная а определяется из условия: от края диска при g=g напряжение<ZG равно нулю. Есть: 3+R То есть А=-^~^Г1=П. Присвоим этому значению L, А B=0 в уравнении получим: (357) и (35.8), (35.16)) И (35.17)) г УЛ/ Соответствующие кривые изменения a®=-и a}= — 1 показаны на рисунке. 587 (кривые f h и fed). Оба напряжения положительны при всех значениях p и увеличиваются по мере уменьшения p, то есть по мере приближения к центру диска. При P = 0(’Алах=(’Апах = Р=Уу’ Гы По радиусу (35.18) Поэтому в диске с очень маленьким
центральным отверстием напряжение на краю отверстия из-за концентрации напряжений в два раза превышает высоту в центре твердого диска[формула (35,14 мм)].) Все рассуждения делаются до сих пор на предположении, что края диска свободны от действия внешних сил. Это предположение обычно не соответствует действительности. Посадка диска на вал вызвана центробежной силой, деформацией отверстия диска, но на внешней кромке диска против него при знаке посадки диска обычно предусмотрен обод для фиксации лопатки турбины, дополнительная центробежная сила передается диску при его вращении. Таким образом, на внешнюю и внутреннюю кромки диска обычно действуют несколько равномерно распределенных растягивающих или сжимающих сил. Напряжение в диске, вызванное этими силами, можно рассчитать по формуле (формула (32.9)§ 197), которая выведена для расчета толстостенных цилиндров. Применяя напряжение в соответствии с уравнениями (32.9), (35.9) и (35.10), можно полностью понять распределение напряжений во вращающемся диске.
и внутреннюю кромки диска обычно действуют несколько равномерно распределенных растягивающих или сжимающих сил. Напряжение в диске, вызванное этими силами, можно рассчитать по формуле (формула (32.9)§ 197), которая выведена для расчета толстостенных цилиндров. Применяя напряжение в соответствии с уравнениями (32.9), (35.9) и (35.10), можно полностью понять распределение напряжений во вращающемся диске.
Смотрите также:
| Расчёт вращающегося кольца (обод маховика) | Диск равного сопротивления |
| Напряжения в спарниках и шатунах. | Влияние резонанса на величину напряжений |

