Вращение твердого тела вокруг неподвижной оси

Вращение твердого тела вокруг неподвижной оси

• Вращение твердого тела вокруг неподвижной оси Простейшим движением твердого тела является поступательное движение и вращение твердого тела вокруг неподвижной оси. Поступательное движение твердого тела-это движение, при котором прямая линия, проведенная на теле, всегда параллельна исходному направлению.

Траектория этой точки движения совпадает с кривыми, полученными друг от друга при переводе. Постепенное движение скорости и ускорение всех точек твердого тела в данный момент геометрически равны. Поэтому при исследовании поступательного движения твердого тела достаточно определить движение 1 точки На теле.

Задача о поступательном движении твердого тела сводится к задаче кинематики точек. Людмила Фирмаль

Если твердое тело вращается вокруг неподвижной оси, то точки на оси вращения неподвижны, а остальные точки представляют собой окружности, центр которых находится на оси вращения и радиус которых равен длине перпендикуляров от точки до оси вращения. Эти окружности находятся в плоскости, перпендикулярной оси вращения. 7) найти общее ускорение точки по величине и направлению, от нормального ускорения и тангенциального ускорения найдено. 2.

второй тип задачи-угловое ускорение или угловая скорость твердого тела является specified. It необходимо найти уравнение вращения, скорости и ускорения твердых точек. 1) интегрирование дифференциальных уравнений, определяющих проекцию углового ускорения на ось вращения. Найти проекцию угловой скорости. Любая интегральная константа определяется из исходных данных. 2) при интегрировании дифференциального уравнения, определяющего проекцию угловой скорости на ось вращения, находим уравнение вращения твердого тела.

• Любая интегральная константа определяется из исходных данных. 3) вычислите величину скорости и нормальное ускорение точки, используя уравнение проекции угловой скорости на вращающуюся ось. 4) определить величину тангенциального ускорения точки, знать проекцию углового ускорения на ось вращения, а затем найти максимальное ускорение точки. Задача 4.1. В 1957/10/4 году искусственный спутник Земли, запущенный в Советском Союзе, первоначально имел революционный период в 1 час 36 минут.

Определите его среднюю частоту циркуляции. Во сколько раз частота вращения спутника превышает угловую скорость Земли(когда Земля вращается вокруг собственной оси)? Решение. . Время эго составляет 1 час 36 минут, то есть 96 минут. Таким образом, радиус-вектор спутника равен П = 96°^!MllH-значение этой частоты вращения в секундах » х： ж = ж% ы-1 = 2м с〜 ’= ° ’ 00109 с «- Величина угловой скорости Земли при вращении вокруг земной оси вращения соответствует 24-1 вращению за 1 час. Или рН = — об / мин = об / мин = об / мин; мин.

Период вращения спутника — это время 1 полного вращения на орбите Людмила Фирмаль

Кроме того, найти отношение частоты вращения Снука к угловой скорости Земли 24•60. Спутник » создает 15 круглых отверстий в течение дня, в течение которых Земля вращается 1 вокруг своей оси. Задача 4.2.Сохраняя состояние предыдущей задачи, учитывая ее траекторию, определяют скорость и ускорение спутника Круговая, высота полета h = 970 км. Радиус Земли равен R = 6370 км.

Решение. Значение скорости спутника определяется по формуле в =(з-р)ч v = {970 + 6370)^ км / с = 8 км / с Через спутник Поскольку тангенциальное ускорение спутника равно пуле (u> = const), величина ускорения равна з = ЗП =(ч + р) П2 =(970 + 6370)= 0.00874 км / с * = = 8,74 м / с \ Ускорение направлено к центру Земли. Задача 4.3.Когда трамвай выстрелит, советник постепенно выключит rheostat.

As в результате угловое ускорение ротора двигателя увеличивается пропорционально времени, и через 6 секунд его угловая скорость достигает 36t: cere’1. Найти количество оборотов, которые Ротор сделал за это время. Решение. Коэффициент углового ускорения е увеличивается пропорционально time. So, если обозначить неизвестный коэффициент пропорциональности буквой k, то получим: Где h + R-радиус circle. So …

Задача 4.2. Интегралом умножив обе стороны уравнения на dt, находим проекцию угловой скорости Ротора на ось вращения. wr = * — J + C(1） Первый момент* = 0 и> 0r = 0, потому что Ротор был неподвижен. Когда вы присваиваете простое значение выражению (I), потому что это C = O、 кт3. С другой стороны, согласно условиям, при t = 6ceK угловая скорость достигает значения, а> 1 = 36 tsec sec’1.Используя это, из Формулы(2)

Определите коэффициент k. 36 тыс. Или к:= Если ввести это значение в Формулу(2), то оно будет выглядеть так: Вт,= м (3） Учитывая интеграцию с=, вы можете увидеть следующее: ТЗ. ？ =- В-р Но при t = 0 угол поворота неподвижного Ротора стал равен пуле (o = 0). Таким образом, C = 0, в конце Тл%/ ИЖ (4） чтобы определить скорость вращения ротора B se, установите T = B sec в(4).

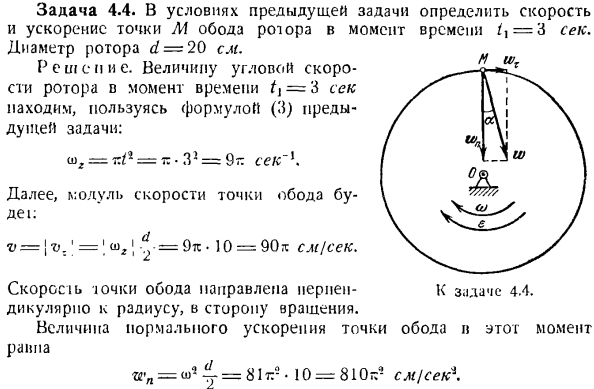
Угол поворота в радианах г•6 Поэтому Ротор за 1 секунду сделал следующее N \ = ^ = = 36 оборотов. 71. Задача 4.4.In по условиям предыдущей задачи определите скорость и ускорение точки М обода ротора в момент времени/,= 3 секунды. Диаметр ротора d = 20 см. Решение: значение угловой скорости Ротора в момент времени t = 3 с получено по формуле (3) предыдущей задачи. = = = ССК \ Далее, модуль скорости точки будайрим v = \ v.\ = \ = т 

Задача 4.6.При подъеме элеватора угловое ускорение барабана с диаметром d = 0,8 м Трос для подъема подставки наматывается и изменяется в соответствии с графиком, показанным на рисунке. Определите максимальную скорость подъема (10 подъемов) и высоту подъема за 20 секунд. Решение. Движение листьев делится на 3 этапа.

В течение первых 2 секунд барабан начинает двигаться из неподвижного состояния и вращается с постоянным угловым ускорением. Поэтому его угловая скорость равна ко-е /、 (1） А угол поворота определяется по формуле _e * 2 9 тонн• предполагая, что t = 2 секунды, вы найдете модуль угловой скорости в конце первой фазы движения а)т = 0.4.2 = 0,8 секунды-1 Величина скорости точек на поверхности барабана равна модулю скорости намотки

На следующем 2-м этапе угловое ускорение пули равно, а угловая скорость барабана не изменяется, поэтому это самая высокая скорость подъема. Поэтому скорость подъема лифта сохранит свое значение. Определите путь, пройденный лифтом и первые 2 seconds. To сделайте это, выяснив по углу поворота барабана за это время (1 0.4 * 22 L 0, 9,= — r> — = 0, s счастливый И поднимаясь высота Л | = АВ г = 0,32 м. На 2-й ступени скорость лифта постоянна и определяется уравнением(2).

Таким образом, высота подъема этой ступени выглядит следующим образом: FН-в (ТС>-ТХ)= 0.32.16 = 5.12 м На третьем этапе вращение барабана происходит при постоянном угловом deceleration. So угол поворота был бы sra = » 1 (*a-U) — = 0,8-2 — = 0,8 рад. Теперь вы можете легко найти лифт лифт на этом этапе. // 3 =?3 ^ = 0,8-0,4 = 0,32 м

Таким образом, общая высота подъема ч = ч {- Джей — Джей — = 5.76 м. Задача 4-7.Вал, к которому крепится пластина вращается в подшипнике по формуле 9-1П(с -¥). «О. Коэффициент. К задаче 4.7.От угловой скорости до 1 Где(1&Z _ » H (?） dt. 1-1.- В * а. м. Или путем сравнения(2)и(1)、 г а. Проекция углового ускорения отрицательна, а проекция угловой скорости вала неограниченно уменьшается со временем. Определить скорость и ускорение центра плиты.Коэффициент скорости в этой точке 1 + ^ Ф 1 а

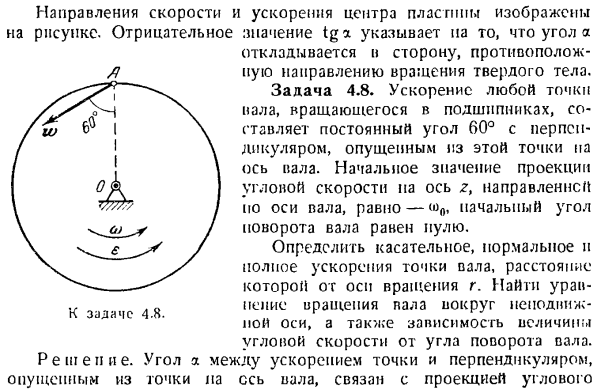
Ускорение в этой точке является суммой нормального ускорения и тангенциального ускорения.Нормальное ускорение Проекция ускорения на касательную определяется по формуле Ч н * н <0-и » ID Полный Модуль Ускорения в = VT + S =£7-BHF \ д Угол a, который состоит из ускорения точки с радиусом, соединенным с осью вращения, выводится из уравнения ы, я Направление скорости и ускорения центра пластины показано на рисунке. отрицательным значением tga является угол a Он расположен в противоположном направлении от направления вращения твердого тела.

Задача 4. 8.Ускорение любой точки вала, которая вращается в подшипнике, составляет постоянный угол 60°, свисающий от этой точки к оси вала.Начальное значение проекции угловой скорости на ось z, направленную вдоль оси вала, равно- З. Или Ш. Затем, исходя из (1) и (4), Определите проекцию углового ускорения на ось вращения e2 = TG пепел!= / с.- (Я.„+Л / 3Ф）“ Проекция ускорения точки, радиус вращения равен R в направлении касательной может быть определена по формуле В * т <н} ш — = тир = — — — м =-. (I-4 — ^ o J / zo2 нормальный коэффициент ускорения этой точки = = — ^В— Тогда значение максимального ускорения точки Вт = Фольксваген% А-Ш \ = 2 к * 2= -.

Чтобы найти уравнение движения вала, воспользуемся уравнением (4) и запишем: // <1-т. Разделите переменные, умножив обе стороны уравнения (5) на dt. — ойн ДТ ОПР = Если я + » в | / 3 * ’интеграции, это выглядит так: 9 + C1 = = — ^ 1n(1 + w0K3 /). (6） Любая интегральная константа C определяется путем подстановки начальных данных формулы(6).Если £= 0, cp = 0, то это C,= 0.Следовательно、 Г, я. 3 1 + o) 01 / sG Это уравнение вращения вала. Определить зависимость угловой скорости вращения от оси проекции проекции на угол rotation.

To сделайте это, умножьте обе части равенство dy(2).Мы это выясним： В РФ 3-ф = — * — г—* о). = р с * ать так〜 С интеграцией, вы можете: Типа VR3> = ЛН для t = 0 0 у> з = — у> 0С 9. Задача 4-9.Регулятор Ватта вращается вокруг вертикальной оси с постоянной угловой скоростью (o). в этом случае угол ASV равен 60°, а ускорение Li B-шара равно 100g по величине-g = 980 см / с*.

Стержни одинаковой длины AC, BC, AD и BD/=] 0 см. Сколько раз регулятор поворачивается за 1 минуту? Решение. Напишите зависимость ускорения шарика от параметров регулятора, чтобы найти величину угловой скорости регулятора. Поскольку регулятор вращается с постоянной угловой скоростью, ускорение шара становится нормальным ускорением, а модуль Или К задаче 4.9. И Да. Она называется уравнением вращения твердого тела вокруг неподвижного естественного around.

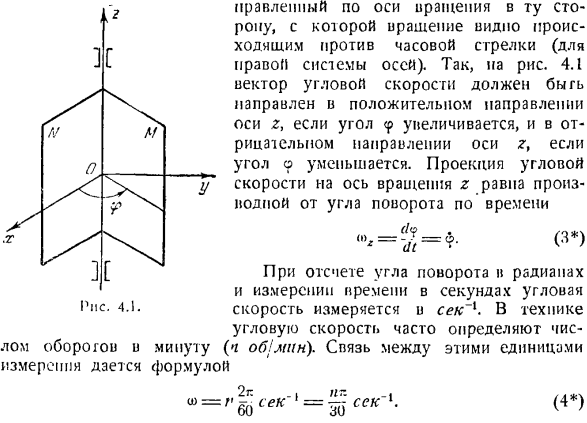
An угол 9 называется угловым смещением твердого тела, которое вращается вокруг неподвижной оси в течение определенного промежутка времени. Угол 9 измеряют следующим образом: рисуют неподвижную плоскость N через ось вращения Oz, неподвижную плоскость Ox, которая соединена с вращающимся телом, подвижную плоскость M и рисуют точку с осью вращения Oz и твердым телом. Тогда двугранный угол между этими плоскостями полностью определяет положение твердого тела(рис. 4.1).

Линейный угол поворота 9 измеряется в радианах или оборотах. 1 вращение соответствует Радиану 2z. Угловая скорость твердого тела характеризует скорость изменения угла поворота твердого тела человека. Угловая скорость является вектором Это определяется по формуле ЗП = ЛШ’2 = = / грех 30co> 2 Где r-кратчайшее расстояние от шара до оси вращения. С другой стороны, в зависимости от условий 100гр.

Если уравнять эти 2 уравнения нормального ускорения шара, то: V / SHI30e-У10. 0. 3 −1™С• В технической системе агрегата угловая скорость регулятора равна РЗВ » и 30 л / 40-30,., 4Р н-ш. — об / мин = — ХЛ — = 1340 об / мин! Минут. 3.14. Овладеть навыком решения задачи о вращении твердого тела вокруг неподвижной оси » И. В. Мещерский, J950 и позже по 375、376、382、385、 386、388、390、393。

Вдоль оси вращения он направлен в направлении, которое, как видно, происходит против часовой стрелки вчера (в случае правой оси).Таким образом, на рис.4.1 вектор угловой скорости направлен в положительное направление оси z при увеличении угла 4, e | = e *. Полное ускорение — это угол a от вертикали, который опущен от точки к оси вращения, а угол a измеряется от ускорения от точки к вертикали(-90°s ^ a ^ 90°). при этом

Часто они указывают направление вращения и углового ускорения с помощью дуговой стрелки W и E(рис. 4.2).Направление стрелки дуги») указывает направление вращения и определяет направление скорости всех точек твердого тела(рис. 4.2). Если стрелки w и e дуги находятся в одном направлении, вращение ускоряется и угловая скорость твердого тела увеличивается. Если стрелки w и e дуги противоположны, то вращение будет медленнее, а угловая скорость твердого тела уменьшится. Направление е определяет направление тангенциального ускорения точки твердого тела(рис. 4.2).

В данном разделе решается задача определения проекции углового и углового ускорения твердого тела на вращающийся вал по заданному уравнению движения. Эта задача приводит к получению производной угла поворота по времени. Обратной задачей является определение закона вращения твердого тела вокруг неподвижной оси. e»: известно угловое ускорение или угловая скорость.

Эта задача решается интегрированием и последующим определением любой постоянной интегрирования в зависимости от начальных условий движения. Зная угловое и угловое ускорение твердого тела, можно определить скорость и ускорение отдельных точек твердого тела, вращающихся вокруг неподвижного шпинделя. Рисунок 4.2. Целесообразно придерживаться такой последовательности действий при решении как жестких задач, так и вращений вокруг неподвижной оси.

Первый тип задачи-уравнение вращения твердого тела является given. It необходимо определить угловую скорость, угловое ускорение, скорость и ускорение точек твердого тела. •1) Выберите систему координат так, чтобы 1 (ось z для наглядности) оси совпадала с осью вращения. 2) составьте уравнение вращения твердого тела (зависимость угла поворота от времени).

3) дифференцирует угол поворота во времени и определяет проекцию угловой скорости на ось вращения. 4) вычислите производную 2-го порядка угла поворота относительно времени, вы найдете проекцию углового ускорения на ось вращения. 5) вычислить линейную скорость точки и ее нормальное ускорение, используя уравнение проекции угловой скорости на вращающуюся ось. 6) определите тангенциальное ускорение точки, используя проекцию углового ускорения на ось вращения.

Смотрите также:

Предмет теоретическая механика

Траектория и уравнения движения точки	Преобразование простейших движений
Скорость и ускорение точки	Абсолютное, переносное и относительное движения точки