Оглавление:



Вращающиеся стержневые системы
- Поворотная система Инерционные нагрузки, направленные на другую сторону ускорения, являются приемлемыми для расчета. Сила распределенной инерционной нагрузки. уы2РР1 ~~ г Q
Сосредоточенная масса усилия г Ка-г (S.4) (10.5) Где со — угловая скорость вращения. R — расстояние от оси вращения. Пример. 1. Штанга постоянного сечения с площадью F,
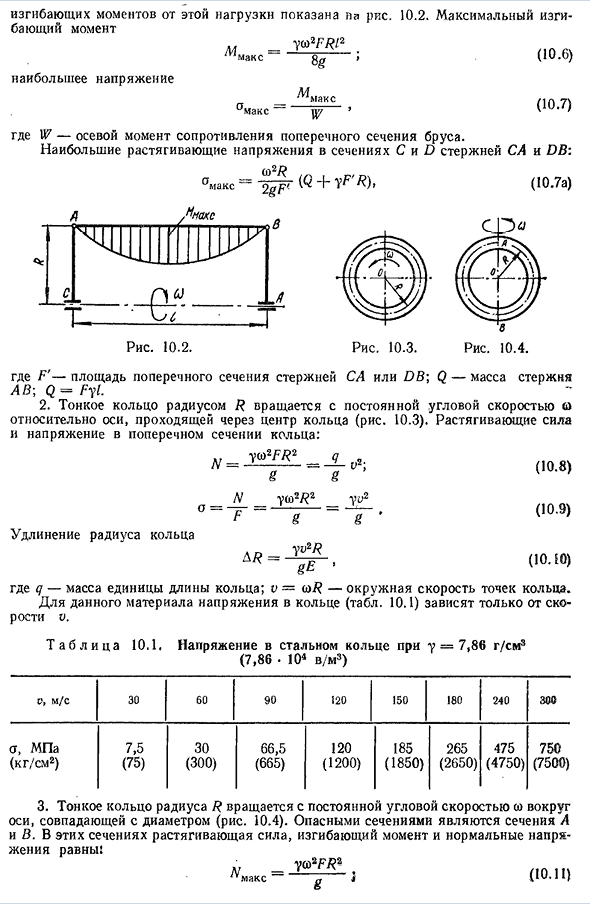
повернутая в точках A и B (рис. 10.2), вращается с постоянной угловой скоростью®. Равномерно Людмила Фирмаль
распределенная сила инерционной нагрузки -i. участок На рисунке показан изгибающий момент 218 из-за этой нагрузки. Момент разрушения _ ya3FRl2 «Gg> в порядке Максимальное напряжение M ”является ак с м м кс п / 10,2. Максимальный изгиб (10.6) (U.7) Где IF — осевой момент сопротивления поперечного сечения балки.
Максимальное растягивающее напряжение в участках C и D стержней CA и DB: Где F ‘- поперечное сечение стержня CA или DB. Q — масса стержня AB-Q = Fyl. 2. Тонкое кольцо с радиусом 7? Он вращается с постоянной угловой скоростью а относительно оси, проходящей через центр кольца (рис. 10.3). Усилие растяжения и растяжения в
- поперечном сечении кольца: N = Yto2f /? 2 = q г г о == Расширение радиуса кольца / V _yy2 /? 2_yy2 P ~ g ~ T (10.8) (10,9) (10.10) Где q — масса единицы длины кольца. v = <$ R — периферийная скорость кольцевой точки. Для данного материала напряжение в кольце (таблица 10.1)
зависит только от скорости V. Таблица 10.1 Напряжение стального кольца при y = 7,86 г / см3 (7,86 • 104 об / м3) V, м / с 30 60 90 120 150 180 240 300 o, МПа 7,5 30 66,5 120185265475 75 ”(кг / см2) (75) (300) (665) (1200) (1850) (2650) (4750) (7500) 3. Радиус тонкого кольца R соответствует диаметру (Рисунок 10.4) Опасными участками являются участки А и В. В этих участках растягивающая сила, изгибающий момент и нормальное напряжение равны. , Y tfF R 2 N, максимум g 1 (S L) 219 лет hmax ♦ _ ^ max |
^ m ax r max «r I ed / (10.12) (10.13) 4. N rp a r n n g i s p p e p. Двойное положение (рис. 10.5) опасно, и его диапазон составляет ± 90 °. В этом случае сила инерции в Людмила Фирмаль
направлении соответствует весу пары. Суммарная интенсивность нагрузки равна uV q = </ + i. Где q ‘= yF — двойная линейная масса. я — г-р-р-линейная сила инерции. £ tgttttttp HHI HH lu ll Рисунок 10.5. Рисунок 10.6. Двойник AB считается простым пучком, нагруженным равномерно распределенной нагрузкой q. Максимальный изгибающий момент в центре двойника М’а с UV72 8 (10.14) Максимальное нормальное напряжение _ ^ m топор _ y I 2 /. , (O2G и макс — 8G V г 5. Нет, и я в т в. В опасном положении, если шатун перпендикулярен кривошипу (рис. 10.6), ускорение пропорционально расстоянию x от центра B. Предполагается также, что масса шатуна
равномерно распределена вдоль его оси. С этими допущениями интенсивность распределенной нагрузки, которая изменяется вдоль треугольника, почти определяется (см. Рисунок 10.6). (10.15) yco2V7? х 1 Где V — объем шатуна. Максимальный изгибающий момент сечения x = -p == = 0,577 I из сечения B: М = О 064 » max u´u ”g И максимальное нормальное напряжение: _ M «макс G 8 (10.16) ° Максимум (10.17)
Смотрите также:
| Частные случаи | Вращающийся диск постоянной толщины |
| Поступательное движение стержня | Колебания упругих систем с одной степенью свободы |

